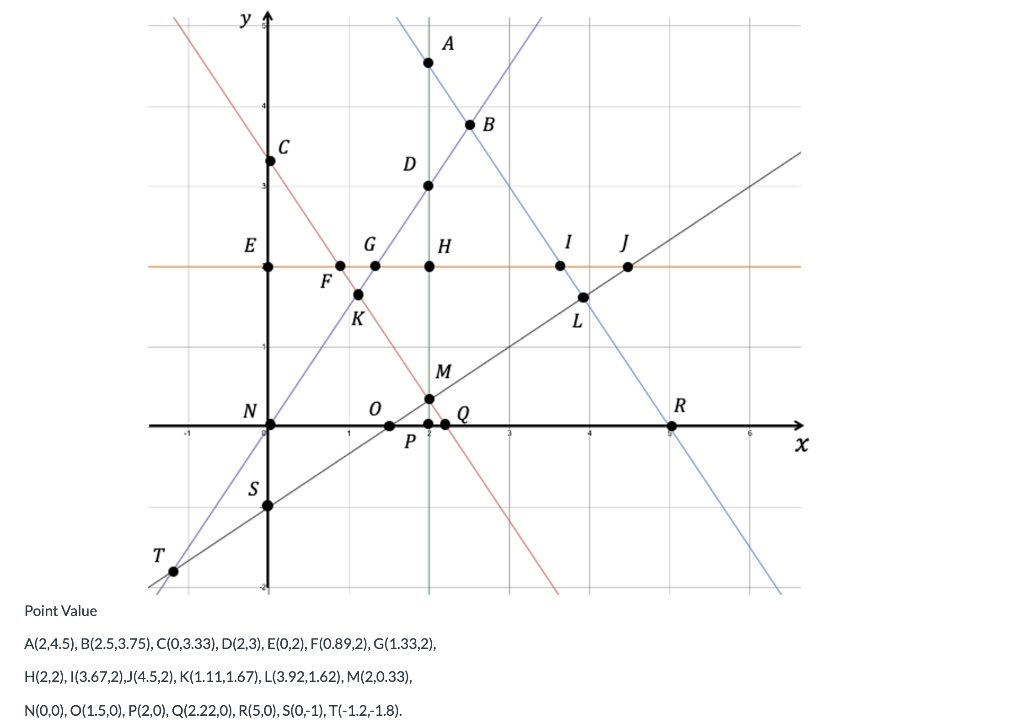
1 10 points An optimization programming model is formulated and the constraints thereof are illustrated as follows: = Max. Z = x + 10y s. t. 3x + 2y = 15 6x 4y > 0 y = 2 9x + 6y > 20 2x 3y > 3 x 22 x, y > 0 The constraints in the model are illustrated in the following plot. y A B D E G H 1 J F K L M N 0 R P x S T Point Value A(2,4.5), B(2.5,3.75), C(0,3.33), D(2,3), E(0,2), F(0.89,2), G(1.33,2), H(2,2), (3.67,2),J(4.5,2), K(1.11,1.67), L(3.92,1.62), M(2,0.33), N(0,0), O(1.5,0), P(2,0), Q(2.22,0), R(5,0), 5(0,-1), T(-1.2,-1.8). Question 1. (i) As a linear programing (LP) model, identify the feasible solution area by determining its extreme points. O Feasible area with Extreme Points (G,F,K) Feasible area with Extreme Points (L,M,Q,R) Feasible area with Extreme Points (B,D,H,L) Feasible area with Extreme Points (G,H,K,M) OJO Feasible area with Extreme Points (1,G,K,M,L) Feasible area with Extreme Points (H,1,L,M) 2 5 points Question 1. (ii) Based on the feasible solution area of the LP model in (i), find all the possible integer solution points for an integer programming (IP) model. (2,1).(2.2).(3,1),(3,2) O (1,2) o (2,2),(2,3),(3,2),(3,3) O (2,1),(2,2).(2,3),(3,1),(3,2).(3,3) (0,0),0,1),(0,2) O (3,0),(3,1),(4,0),(4,1),(5,0) 3 5 points Question 1. (iii) Find the optimal point and compute the optimal objective values in LP. X = 3.92, y = 1.62, z = 20.12 x = 1.33, y = 2, z = 21.33 x -4.5, y = 2, z = 24.5 X = 3.92, y = 1.62, z = 16.88 X = 0.89, y = 2, z = 20.89 17 110,0 Dooo (2,1),(2,2),(2,3),(3,1),(3,2),(3,3) (0,0),(0,1),(0,2) (3,0),(3,1),(4,0),(4,1),(5,0) 3 5 points Question 1. (iii) Find the optimal point and compute the optimal objective values in LP. x = 3.92, y = 1.62, z = 20.12 x = 1.33, y = 2, z = 21.33 X = 4.5, y = 2, z = 24.5 OOOO x= 3.92, y = 1.62, z = 16.88 x = 0.89, y = 2, z = 20.89 X = 1.11, y = 1.67, z = 14.47 X= 4.5, y = 2, z = 20.5 x = 1.11, y = 1.67, z = 17.81 4 5 points Question 1. (iv) Find the optimal point and compute the optimal objective values in IP. x = 4, y = 0, z = 4 x = 4, y = 1, z = 14 X= 5, y = 1, z = 15 x = 3, y = 1, z = 13 X = 3, y = 2, z = 19 x = 5, y = 0, z = 5 x = 4, y = 1, z = 12