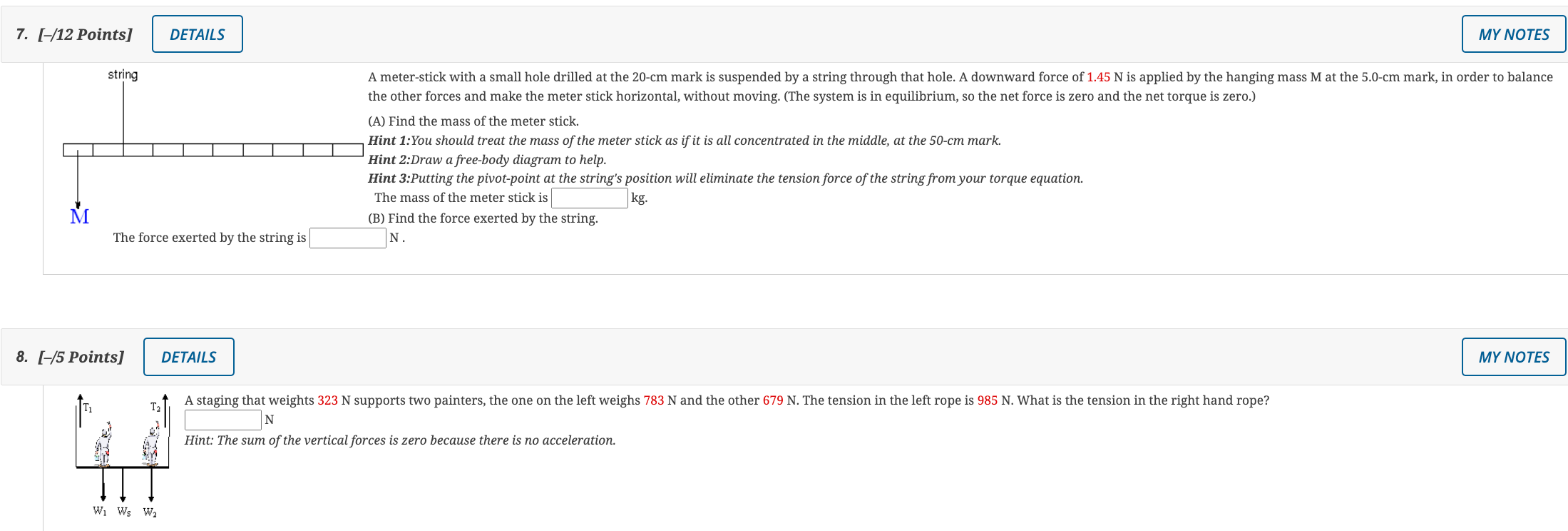
1. [/12 Points] MY NOTES We consider a solid ball of mass 0.29 kg and radius 9 cm, rolling down an inclihe without slipping. Suppose the ball starts from rest and rolls enough that it drops vertically by a distance h = 0.67 m. Use conservation of energy to nd the speed v of the hall. The speed is E . Hint: There are two types of kinetic energy related to the ball, Consider replacing the solid ball with a thin-walled hollow sphere with the same mass and the same radius. For the hollow sphere, the speed would be S. The rotational intertiafnrmulnfor a hollow sphere is l = %M R2 The rotational intertiafnrmulnfor a solia' sphere is] = g MR2 Submit Answer 2. [/5 Points] MY NOTES Photo len mecwn mm A 1.90 m radius playground merry-go-rouhd has a mass of 120 kg and is rotating with an angular speed of 2.83 rad/s. A child is holding on at the outer edge. What (minimum) force must the 20.0 kg child use to hold on to the merryrgorround to keep from being slung off? That is, what centripetal force must the child's grasp provide? The child must hold on with a force of at least E. (For comparison the child weighs 196.0 N) 5. [-/5 Points] DETAILS MY NOTES Three children are riding on the edge of a merry-go-round that is 202 kg, has a 1.60 m radius, and is spinning at 21.3 rpm. The children have masses of 19.9, 28.5, and 38.8 kg. If the child who has a mass of 28.5 kg moves to the center of the merry-go-round, what is the new angular velocity in rpm? Approximate the merry-go-round as a solid disk, and each child as a point mass. rpm7. [/12 Points] DETAILS \"Vi"g Ameter-stick with a small hole drilled at the 20-cm mark is suspended by a string through that hole. A downward force of 1.45 N is applied by the hanging mass M at the 5.0-tm mark in order to balance the other forces and make the meter stick horizontal. without moving. (The system is in equilibrium, so the net force is zero and the net torque is zero.) (A) Find the mass of the meter stick. Hint 1:You should treat the mass of the meter stick as if it is all concentrated in the middle, at the 50-cm mark. Hint Z:Draw a free-body diagram to help. Hint 3:Putting the pivot-point at the string's position will eliminate the tension force of the stri ng from your torque equation. The mass of the meter stick is E kg. RI (B) Find the force exerted by the string. The force exerted by the string is E N . 8. [/5 Points] A staging that weights 323 N supports two painters, the one on the left weighs 783 N and the other 679 N. The tension in the left rope is 985 N. What is the tension in the right hand rope? EN Hint: The sum of the vertical forces is zero because there is no acceleration. W] W: W; 9. [/15 Points] 2 Spinning Ice Skater (a) Calculate the angular momentum of an ice skater spinning at 6.00 rev/s ( 37.7 rad/s) given his moment of inertia is 0.4300 kg-m (Moment of inertia is the same quantity as rotational inertia.) |_ = b He reduces his rate of spin (his angular velocity) by extending his arms and increasing his moment of inertia. Find the value of his new moment of inertia if his angular velocity drops to 2.05 rev/s. H i 1 z (c) Suppose instead he keeps his arms in and allows friction with the ice to slow him to 3.00 rev/s ( 18.85 rad/s). What average torque was exerted if this takes 20.0 seconds? H (Hint: consider the torque (and angular acceleration) to be constant so this is an analog to the constant acceleration problems. The torque is negative as it slows a positive rotation speed.) 10. [-/20 Points] DETAILS MY NOTES A pulsar (a rotating neutron star) has a mass of 1.83 solar masses and rotates with a period of 1.893 s. 1 solar mass is the mass of our Sun or 1.988 x 1030 kg. (A) What is the angular speed of the pulsar? w = rad/s (B) We will model the neutron star as a uniform sphere with an effective radius of 9000 m (9 km). With this model what would its rotational inertia be? pulsar (C) What is the rotational (kinetic) energy of the pulsar? KErot = (D) The pulsar loses energy and slows down very slowly. Every second the pulsar's frequency changes by only Af= -3.2650 x 10-13 Hz or Aw =-2.0515 x 10-12 rad/s. This slowing of the rotation is due mostly to energy lost by electromagnetic radiation from the rotating magnetic moment of the pulsar. How much rotational kinetic energy is lost in one second? This is such a small relative change that we would have problems calculating the change in kinetic energy using AKE = KE- KE; (Inaccurate due to numerical computation errors) This inaccuracy is because we are subtracting two numbers that agree to many significant digits. For example if two values agree to 14 significant digits, you would need to calculate their values to 17 significant digits to have 3 significant digits left in their difference. However, it can be shown that the change in rotational kinetic energy can be calculated without huge round-off errors by using AKE = I.W.W. This approximate formula is valid when Aw is very small compared to w. Energy lost in 1 second (AKE) is For a young pulsar this energy 'fuels' the glowing gases in the nebula until they have moved far from the pulsar