Question: 1. (17 points) Consider the following set: S = = { [@PO], where p(t) = at + bt + c. [p(0) p(0)] (A) Show

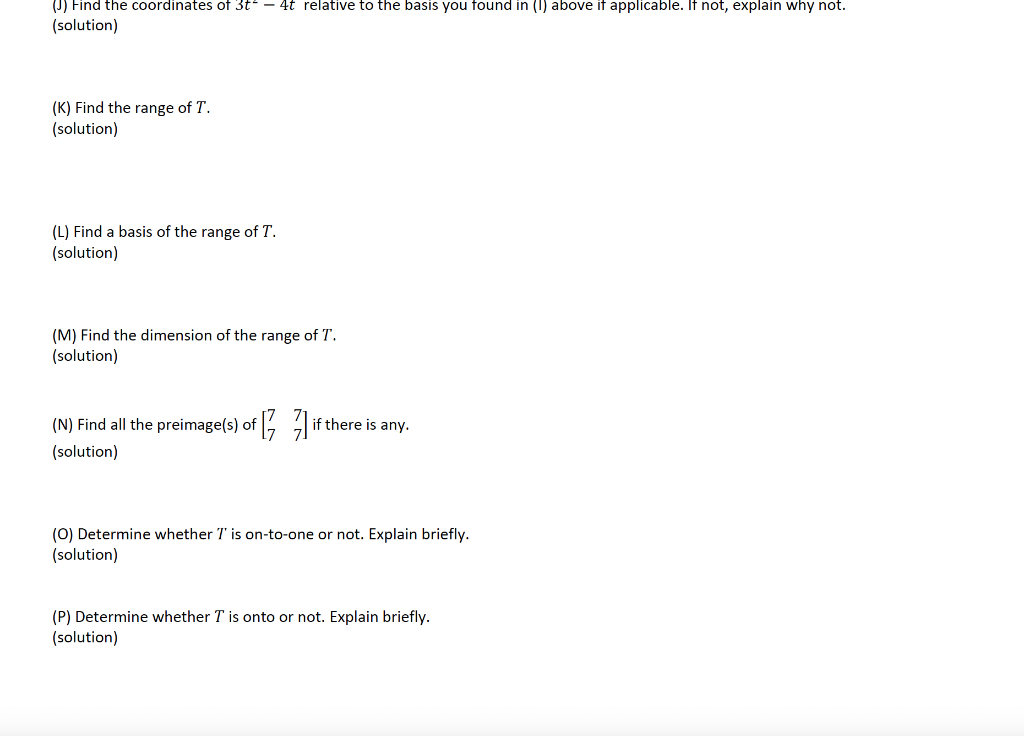
1. (17 points) Consider the following set: S = = { ["@PO], where p(t) = at + bt + c. [p(0) p(0)] (A) Show that the set is non-empty. (solution) (B) Determine whether there exists the additive identity of the set or not. If yes, find it. Otherwise, explain why not. (solution) (C) Determine whether the set is closed under addition or not. Explain why or why not. (solution) (D) Determine whether the set is closed under scalar multiplication or not. Explain why or why not. (solution) (E) Determine whether the set is a vector space or not. Explain why or why not. (solution) (F)-(P) Let T: P2 S be defined by T (p(t)) = PO PO, where P = {at + bt + c, where a, b and c are any real numbers.}, and S is the set defined above. (G) Determine whether T is linear or not. Explain why or why not. (solution) (H) Find the kernel of T. (solution) This is an assessment that must be done with YOUR OWN WORK! This Knowledge Check must be done with YOUR OWN WORK! (1) Find a basis of the kernel of T. (solution) Page 2 of 3 (K) Find the range of T. (solution) WINTER 2023 (J) Find the coordinates of 3t - 4t relative to the basis you found in (1) above if applicable. If not, explain why not. (solution) (J) Find the coordinates of 3t - 4t relative to the basis you found in (I) above if applicable. If not, explain why not. (solution) (K) Find the range of T. (solution) (L) Find a basis of the range of T. (solution) (M) Find the dimension of the range of T. (solution) of [77]ift (N) Find all the preimage(s) of (solution) if there is any. (O) Determine whether T' is on-to-one or not. Explain briefly. (solution) (P) Determine whether T is onto or not. Explain briefly. (solution)

Step by Step Solution

★★★★★

3.36 Rating (152 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock

A To show that the set is nonempty we need to find at least one element that belongs to the set S Lets choose pt 2t2 3t 1 We can see that p0 1 so pt 1 1 2t2 3t 1 Therefore pt 2t2 3t 1 belongs to the s... View full answer

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Mathematics Questions!

Consider the following set of dependent and independent variables. These data can also be found in the Excel file Prob 151.xlsx. a. Using PHStat, construct a regression model using both independent...

Consider the following set of dependent and independent variables. These data can also be found in the Excel file Prob 153.xlsx. a. Using PHStat, construct a regression model using both independent...

Consider the following set of data: a. Use standard stepwise regression to produce an estimate of a multiple regression model to predict y. b. Use forward selection stepwise regression to produce an...

Consider the following set of data points. a. Compute the linear correlation coefficient, r. b. Can you conclude from your answer in part (a) that the variables x and y are unrelated? Explain your...

Consider the following set of dependent and independent variables. These data can also be found in the Excel file Prob 1541.xlsx. Using PH Stat , check for the presence of multicollinearity. If...

The state of Michigan generates a three-digit number at random twice a day, seven days a week for its Daily 3 game. The numbers are generated one digit at a time. Consider the following set of 50...

Consider the following set of voter preferences: a. Compute the plurality winner of the election. b. Compute the Borda winner of the election. c. Compute the Condorcet winner of the election. d....

Consider the following set of hypothetical data: Suppose you want to do a multiple regression of Y on X2 and X3. a. Can you estimate the parameters of this model? Why or why not? b. If not, which...

Consider the following set of cash flows over a four-year period. Determine the NPV of these cash flows if r = 0.15 and cash flows occur at the end of the year. Year 1 2 3 4 Cash flow -$600 $550...

Consider the following set of equations: (i) From first principles, try to solve it. Does this set have a unique solution? (ii) Write the set of equations in matrix-vector form. (iii) Relate the...

the financial statemen th's new manageoe y that Smith's financ Te occurrence of eme a. Which of the following organizations can revoke the right of an individual to practice as a CPA? () The Public...

Bethany got a call yesterday from First Bank, the company that issued her credit card, inquiring about an $ 1 0 5 . 0 0 charge made in Jamaica. Upon learning that Bethany was at home in Minnesota and...

Arya earns $17.20 per hour and works 80.0 regular hours per bi-weekly pay period. In addition, Arya worked 8.5 overtime hours this pay period, which are paid at 1.5 times her regular hourly rate. She...

Use the ML Practitioner Assessment project to answer this question. Which two of the following statements about the "grade" column in the schools_data dataset are true? It has a mean of 10.56 and a...

= CPPREP4104 Establish buyer re lationships -NSW ? Item 10 of 13 You have received two (2) first home buyer enquiries via email - they have both filled out a buyer profile. Open and read through...

Use the ML Practitioner Assessment project to answer this question. Classification models establish a certain probability as a threshold. In the Evaluate recipe, if the model assigns a probability to...

Huron Company produces a commercial cleaning compound known as Zoom. The direct materials and direct labour standards for one unit of Zoom follow: Standard Quantity or Hours Standard Price or Rate...

Use the T account for Cash below to record the portion of each of the following transactions, if any that affect cash. How do these transactions affect the companys liquidity? Jan. 2 Provided...

Find a formula for the general term an (not the partial sum) of the infinite series. a. b. c. d. 3 9 27 81 1 5 25 125 1 22 33 1 21 3 2. 4.3.2.1

What are the two ways of writing the difference quotient?

Plot the function using a graphing utility and find its critical points and extreme values on [5, 5]. 1 1+ x 1|'1+ |x - 4|

Compare two conflicts in which avoiding worked in different ways one conflict you avoided eventually resolved itself, and another you avoided that ended up getting worse because you put off...

Based on your experiences with conflict, what would you say are your assumptions about conflict? How do they affect the way you make choices when you are faced with a problematic situation?

Think of a time when you felt that you handled a conflict well. What did you do that seemed competent to you? How do those behaviors contrast with a time when you felt you handled a conflict poorly?