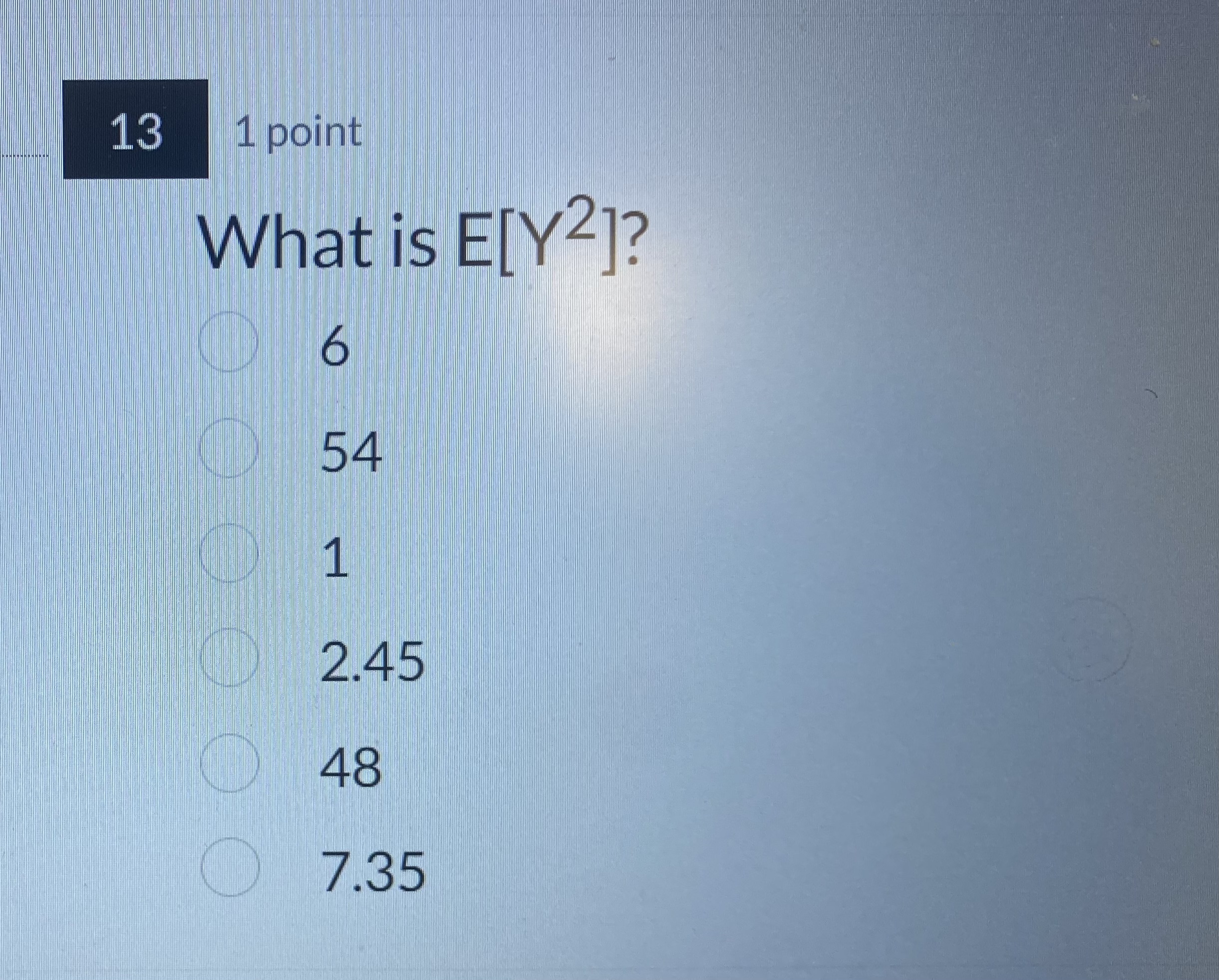
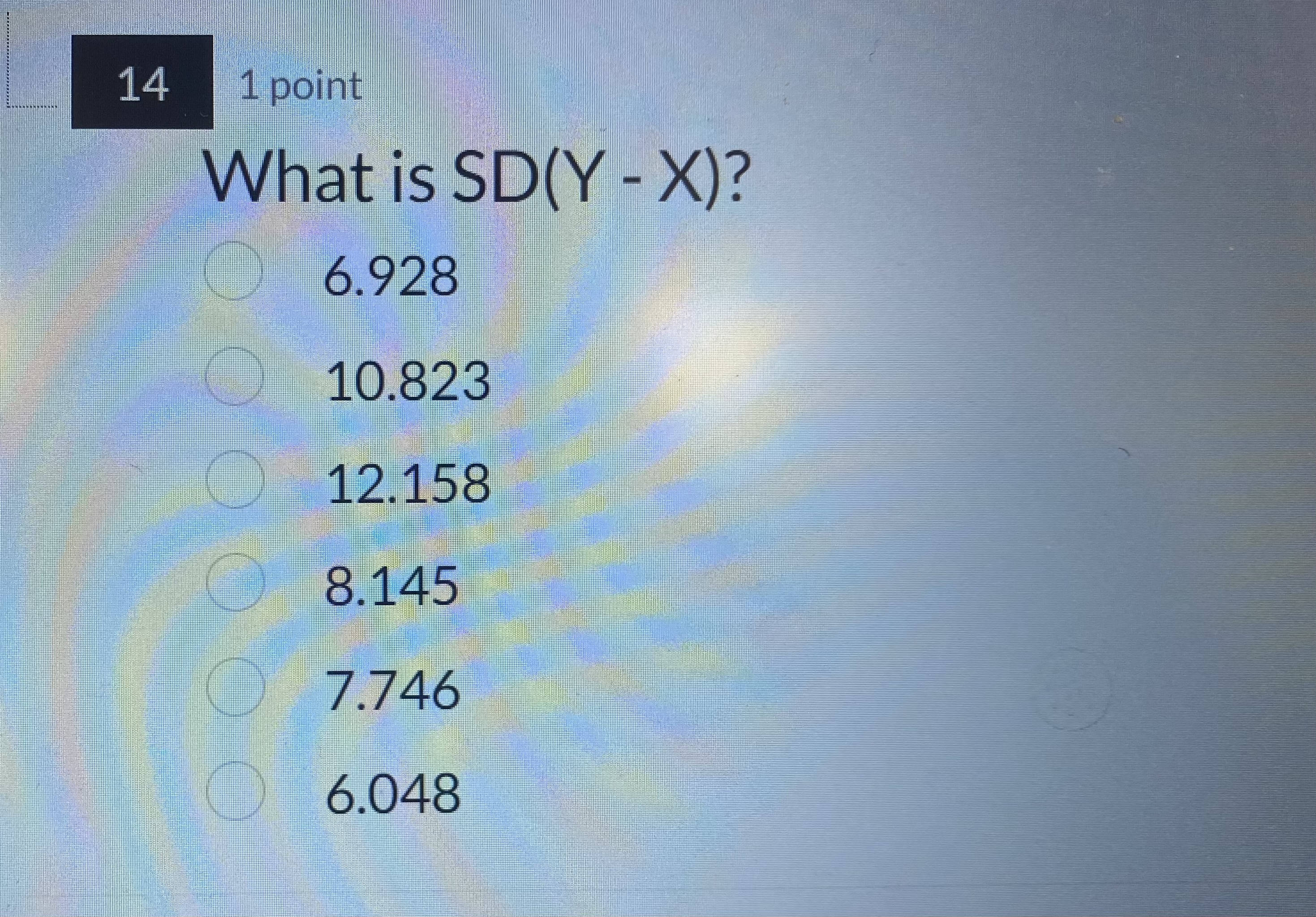
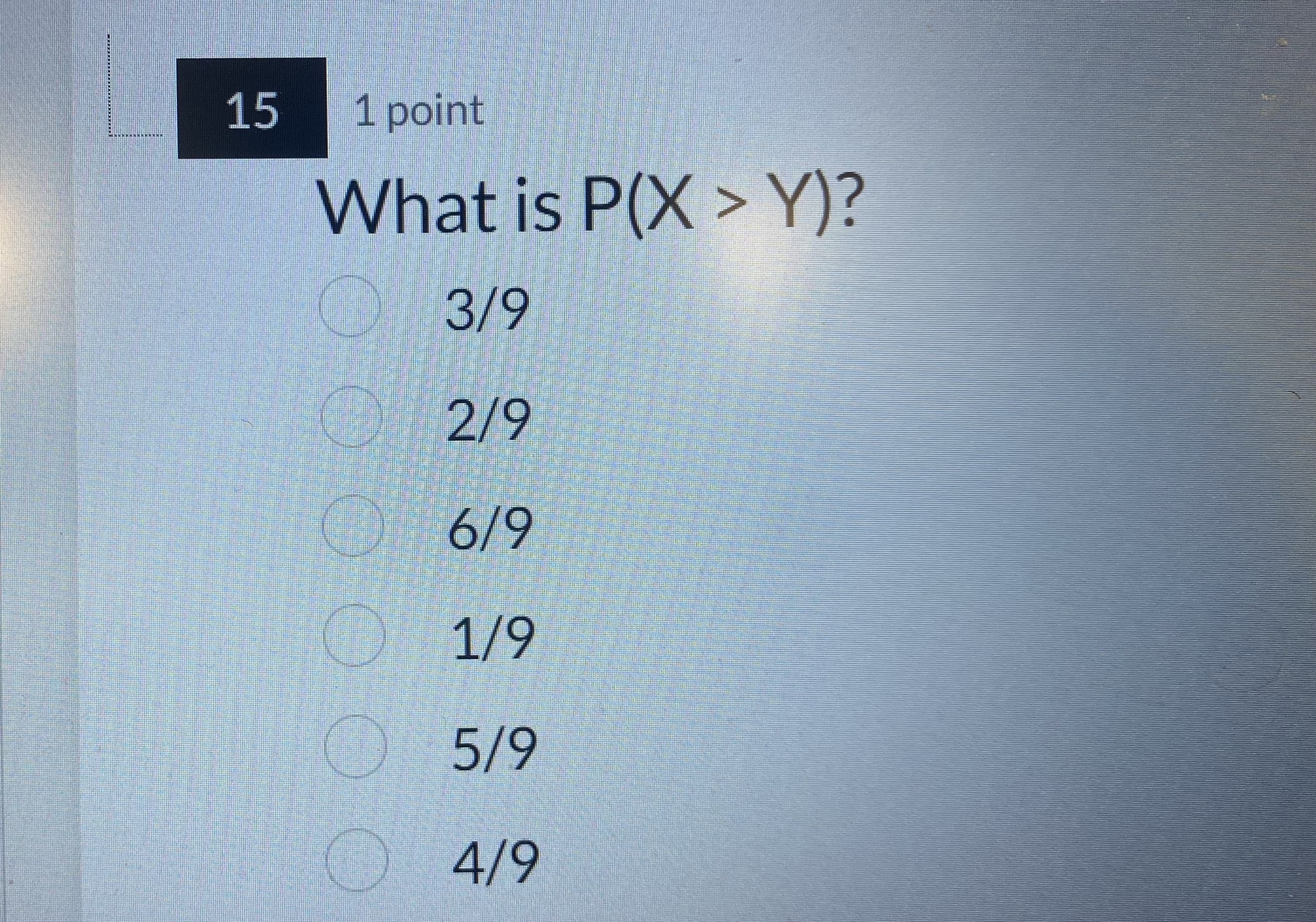
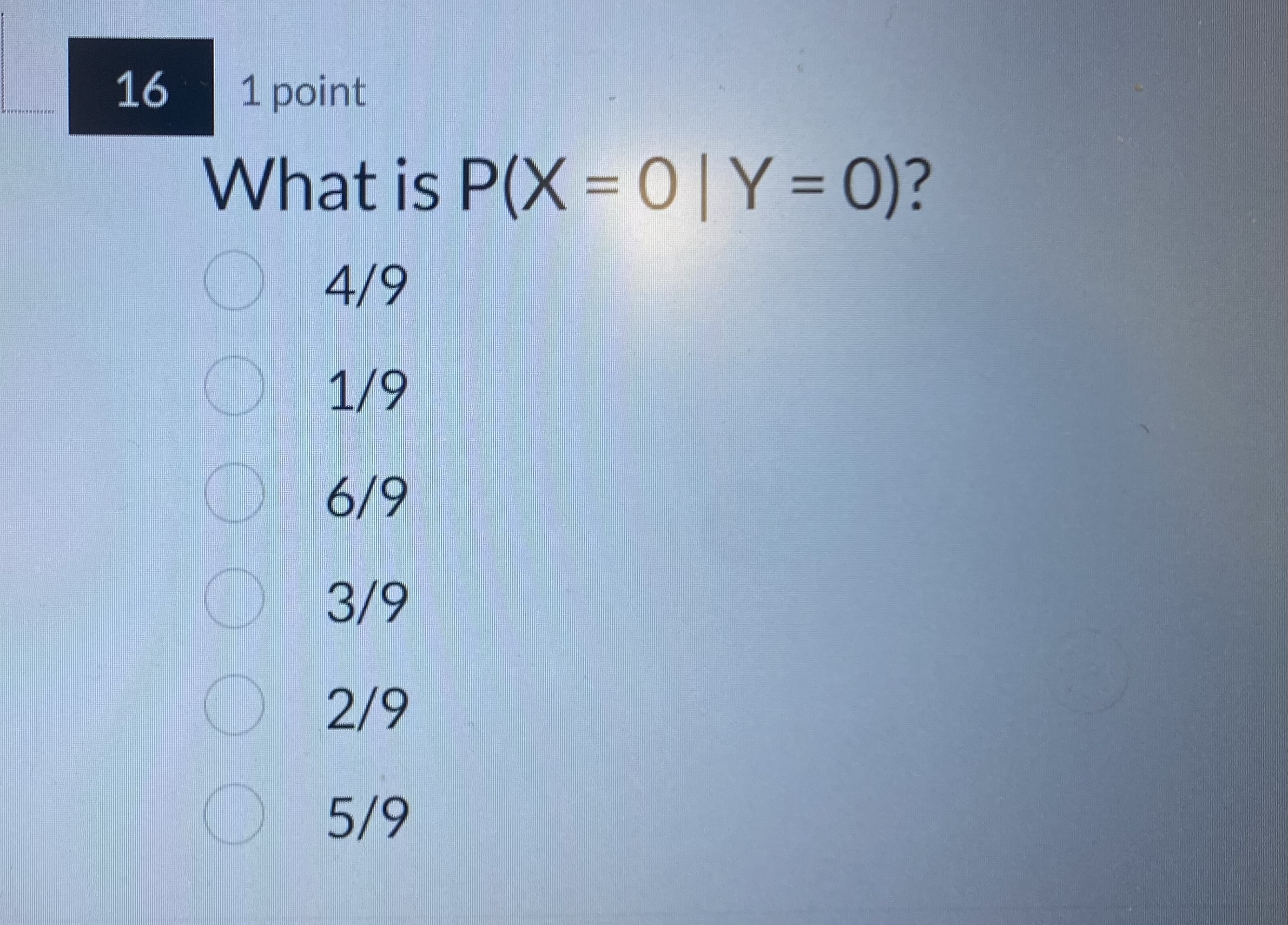
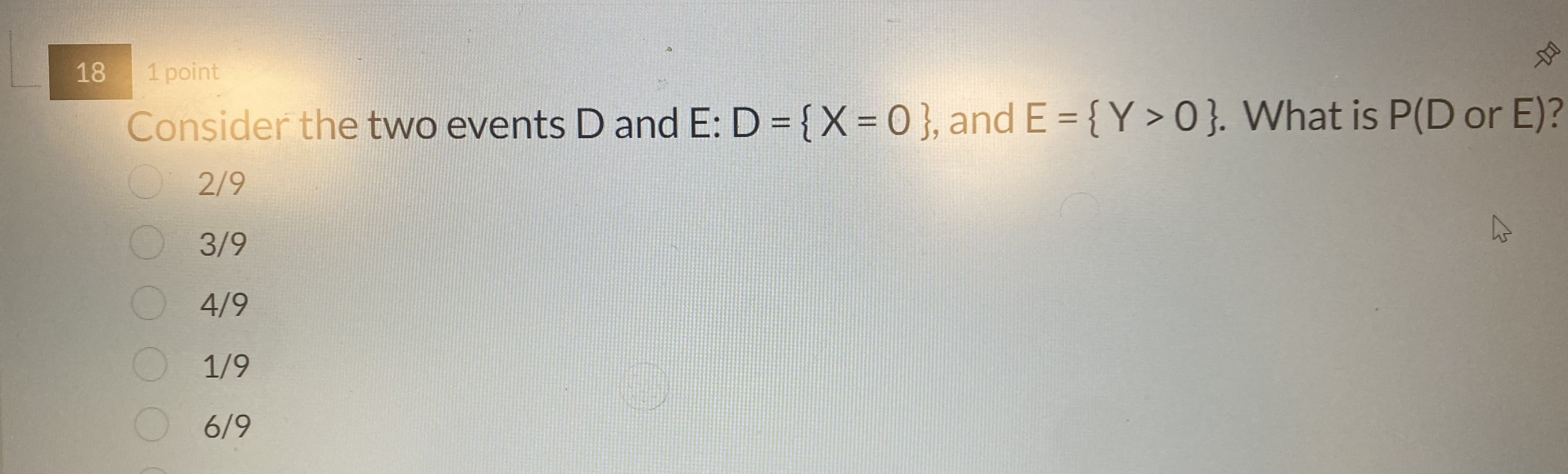
#1 # # # # # # # # # # # # ## ## The joint distribution of X and Y is given below. Note: Var(X) = 6 and Var(Y) = 54. X -3 0 3 -9 1/9 1/9 1/9 1/3 Y 0 1/9 1/9 1/9 1/3 9 1/9 1/9 1/9 1/3 1/3 1/3 1/3 111 1 point Are X and Y independent? Why? Yes, because the joint probabilities add up to 1. O No, because the joint probability distribution is skewed. O Yes, because the marginal distributions of X and Y are both symmetric. O No, because the covariance is not zero. Yes, because P(X = x and Y = y) = P(X = x) P(Y = y) for all x's and y's. No, because X and Y have identical distributions.12 1 point Which of the following statements is true? The covariance between X and Y is 1. The correlation between X and Y is 1. The joint distribution of X and Y is right skewed. O X and Y are identically distributed. O E[X] = E[Y] = 1/3 O E[X] = EMY] = 0\f\f\f\f17 1 point Consider the two events A and B: A = { X = -3 }, and B = { X =0}. The events A and B are: O Mutually exclusive Bayesian Exhaustive O Sample space O Independent O Complementary\f19 1 point X is an example of a: Mixed random variable Discrete random variable O Normal random variable Continuous random variable O Constant random variable Bernoulli random variable\f