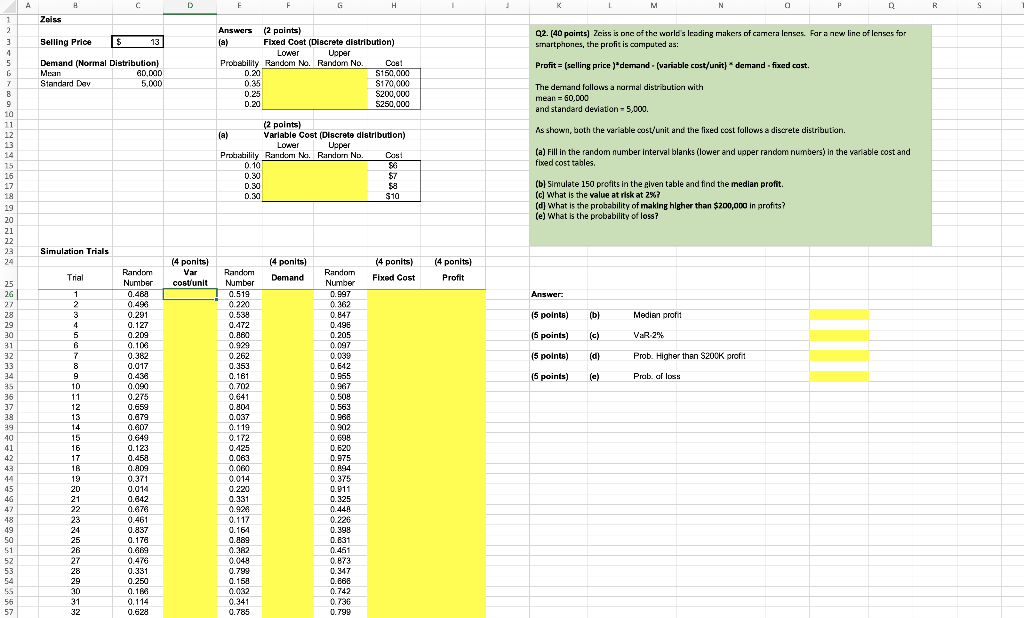
1 2 3 4 5 G 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 2.5 26 27 28 2.9 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 5.5 56 57 A Zeiss Selling Price $ 13 Demand (Normal Distribution) Mean 60,000 Standard Dev 5.000 Simulation Trials Trial 1 2 3 4 5 6 7 8 9 40 10 11 12 13 14 15 16 20 17 16 19 C 20 21 22 23 24 25 26 27 28 29 30 31 32 Random Number 0.468 0.496 0.291 0.127 0.209 0.106 0.382 0.017 0.438 0.090 0.275 0.659 0.679 0.607 0.649 0.123 0.458 0.809 0.371 0.014 0.642 0.676 0.461 0.837 0.176 0.669 0.476 0.331 0.250 0.166 0.114 0.628 D (4 ponits) Var cost/unit E F H (2 points) Answers (a) Fixed Cost (Discrete distribution) Lower Upper Probability Random No. Random No. 0.20 Cost $150,000 $170,000 0.35 0.25 $200,000 0.20 $250,000 (2 points) (a) Variable Cost (Discrete distribution) Lower Upper Probability Random No. Random No. 0.10 Cost $6 0.30 $7 0.30 $8 0.30 $10 (4 ponits) Fixed Cost Random Number 0.519 0.220 0.538 0.472 0.860 0.929 0.262 0.353 0.161 0.702 0.641 0.804 0.037 0.119 0.172 0.425 0.063 0.060 0.014 0.220 0.331 0.928 0.117 0.164 0.889 0.382 0.048 0.799 0.158 0.032 0.341 0.785 (4 ponits) Demand Random Number 0.997 0.362 0.847 0.496 0.205 0.097 0.039 0.642 0.955 207 0.967 0.508 0.563 0.968 0.902 0.698 0.620 0.975 0.894 0.375 0.911 0.325 0.448 0.226 0.398 0.831 0.451 0.873 0.347 0.868 0.742 0.736 0.799 I (4 ponits) Profit J K M N 0 P Q R Q2. (40 points) Zeiss is one of the world's leading makers of camera lenses. For a new line of lenses for smartphones, the profit is computed as: Profit= (selling price )*demand-(variable cost/unit) * demand-fixed cost. The demand follows a normal distribution with mean = 50,000 and standard deviation 5,000. As shown, both the variable cost/unit and the fixed cost follows a discrete distribution. (a) Fill in the random number interval blanks (lower and upper random numbers) in the variable cost and fixed cost tables. (b) Simulate 150 profits in the given table and find the median profit. (c) What is the value at risk at 2%? (d) What is the probability of making higher than $200,000 in profits? (e) What is the probability of loss? Answer: (5 points) Median profit (5 points) VaR-2% (5 points) Prob. Higher than $200K profit (5 points) Prob. of loss (b) (c) (d) (e) S 1 2 3 4 5 G 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 2.5 26 27 28 2.9 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 5.5 56 57 A Zeiss Selling Price $ 13 Demand (Normal Distribution) Mean 60,000 Standard Dev 5.000 Simulation Trials Trial 1 2 3 4 5 6 7 8 9 40 10 11 12 13 14 15 16 20 17 16 19 C 20 21 22 23 24 25 26 27 28 29 30 31 32 Random Number 0.468 0.496 0.291 0.127 0.209 0.106 0.382 0.017 0.438 0.090 0.275 0.659 0.679 0.607 0.649 0.123 0.458 0.809 0.371 0.014 0.642 0.676 0.461 0.837 0.176 0.669 0.476 0.331 0.250 0.166 0.114 0.628 D (4 ponits) Var cost/unit E F H (2 points) Answers (a) Fixed Cost (Discrete distribution) Lower Upper Probability Random No. Random No. 0.20 Cost $150,000 $170,000 0.35 0.25 $200,000 0.20 $250,000 (2 points) (a) Variable Cost (Discrete distribution) Lower Upper Probability Random No. Random No. 0.10 Cost $6 0.30 $7 0.30 $8 0.30 $10 (4 ponits) Fixed Cost Random Number 0.519 0.220 0.538 0.472 0.860 0.929 0.262 0.353 0.161 0.702 0.641 0.804 0.037 0.119 0.172 0.425 0.063 0.060 0.014 0.220 0.331 0.928 0.117 0.164 0.889 0.382 0.048 0.799 0.158 0.032 0.341 0.785 (4 ponits) Demand Random Number 0.997 0.362 0.847 0.496 0.205 0.097 0.039 0.642 0.955 207 0.967 0.508 0.563 0.968 0.902 0.698 0.620 0.975 0.894 0.375 0.911 0.325 0.448 0.226 0.398 0.831 0.451 0.873 0.347 0.868 0.742 0.736 0.799 I (4 ponits) Profit J K M N 0 P Q R Q2. (40 points) Zeiss is one of the world's leading makers of camera lenses. For a new line of lenses for smartphones, the profit is computed as: Profit= (selling price )*demand-(variable cost/unit) * demand-fixed cost. The demand follows a normal distribution with mean = 50,000 and standard deviation 5,000. As shown, both the variable cost/unit and the fixed cost follows a discrete distribution. (a) Fill in the random number interval blanks (lower and upper random numbers) in the variable cost and fixed cost tables. (b) Simulate 150 profits in the given table and find the median profit. (c) What is the value at risk at 2%? (d) What is the probability of making higher than $200,000 in profits? (e) What is the probability of loss? Answer: (5 points) Median profit (5 points) VaR-2% (5 points) Prob. Higher than $200K profit (5 points) Prob. of loss (b) (c) (d) (e) S