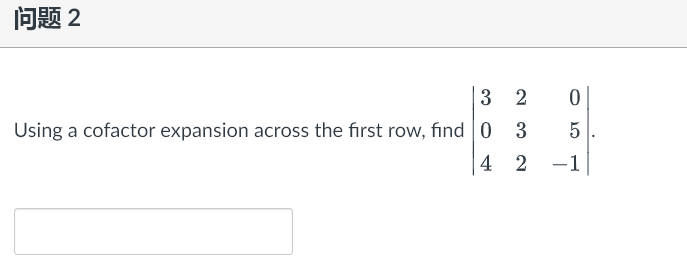
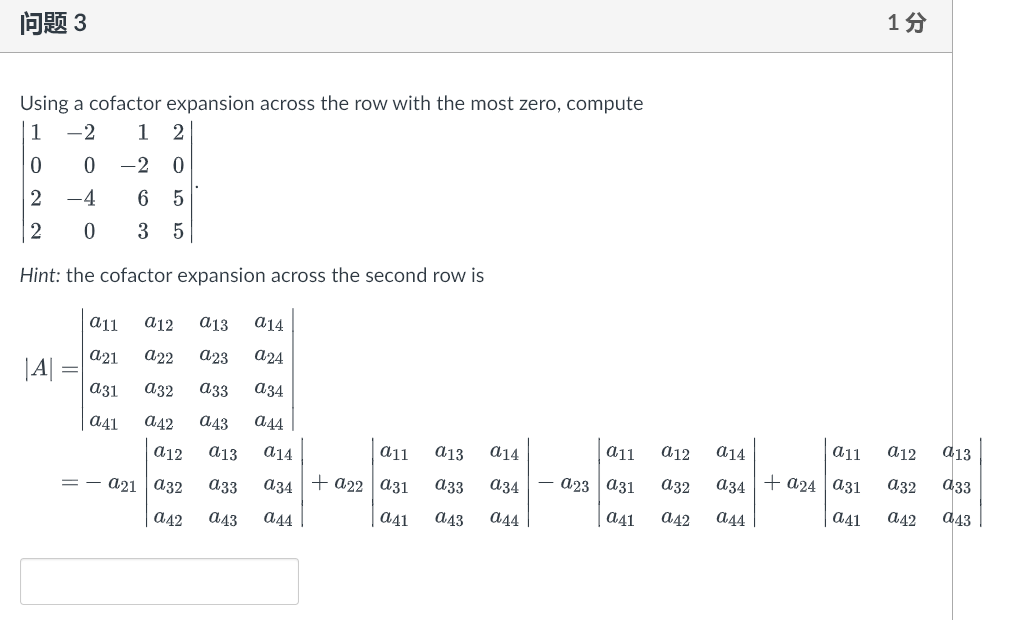
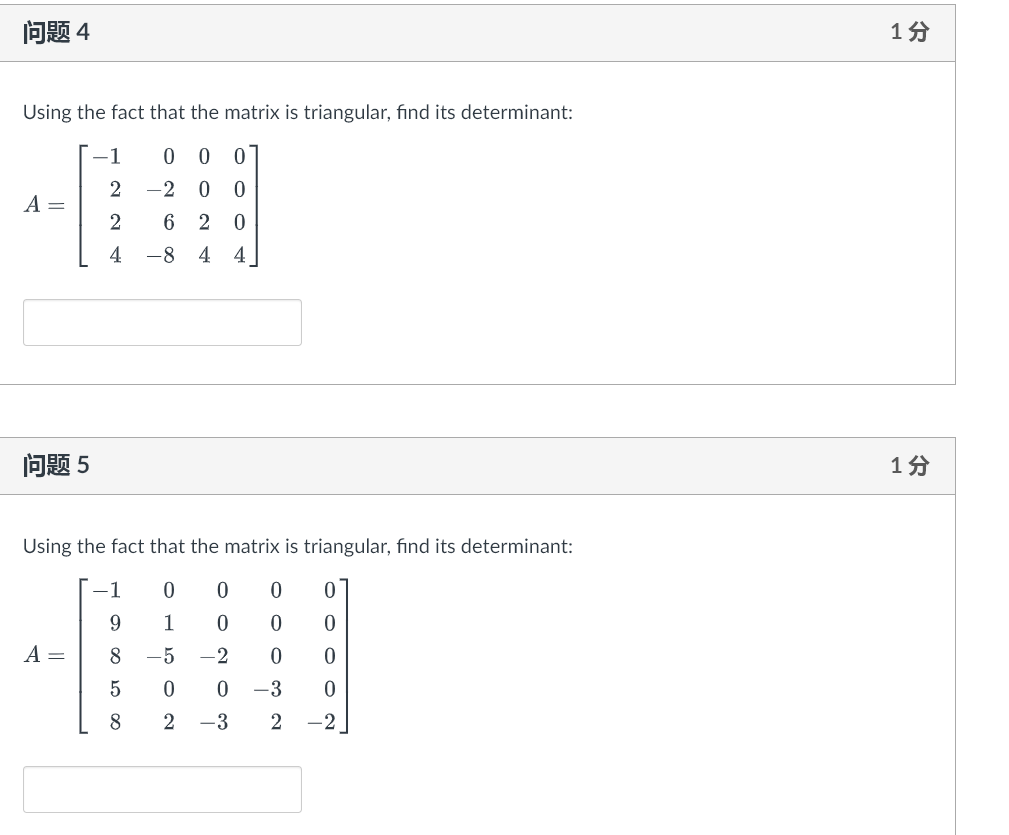
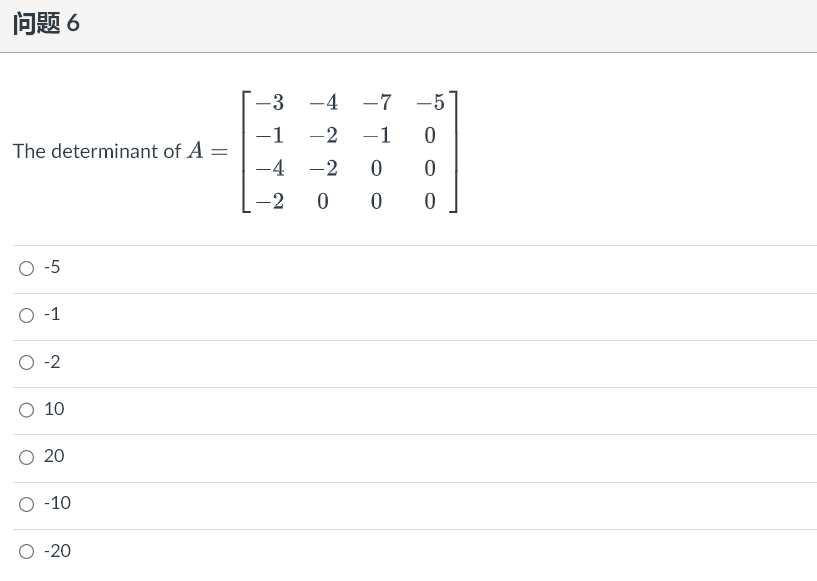
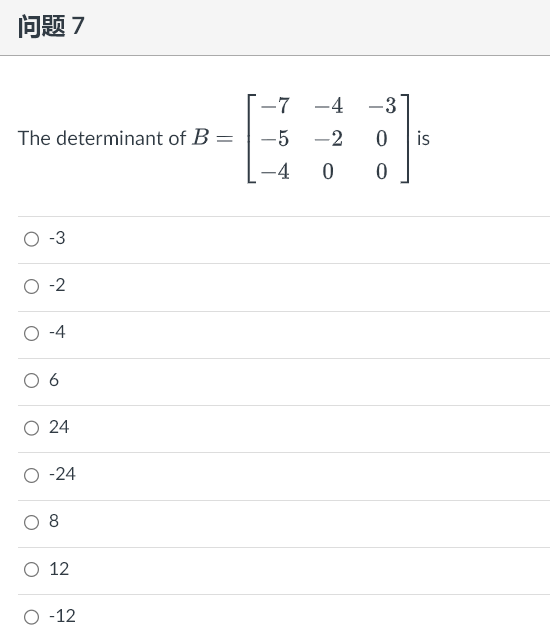
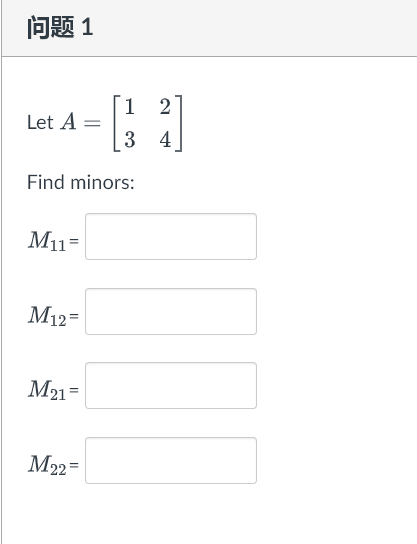
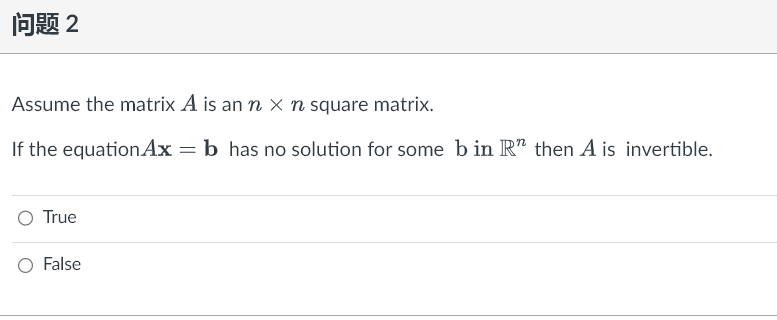
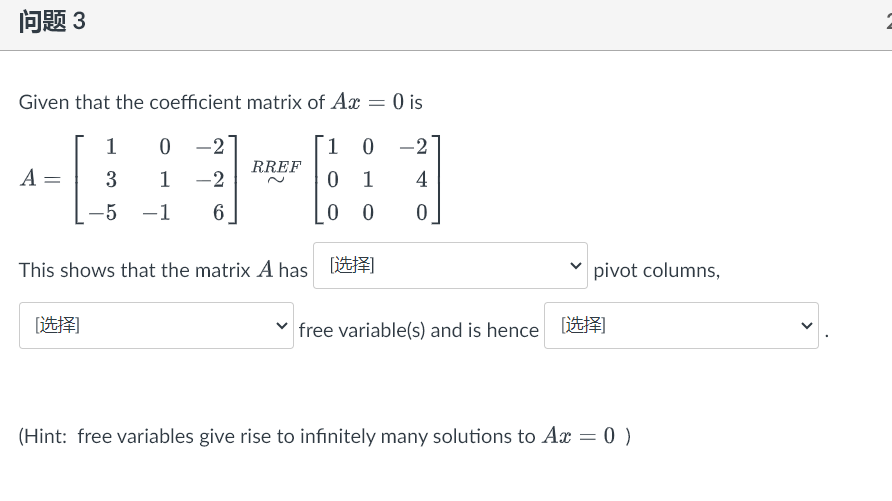
1 2 3 4 OT Using a cofactor expansion across the first row, find 7 8 (Hint the cofactor expansion across the first row is All A12 p13 all A12 013 All 12 213 + a13 a21 a22 A23 - a12 a21 122 a23 a31 A33 |A = all A21 22 a23 a32 a31 A32 a33 A31 a32 a33 a21 a22 a21 a23 a22 a23 + a13 - a12 a31 a32 = all a31 a33 a32 a33\f1 53 Using a cofactor expansion across the row with the most zero, compute 1 -2 1 2 0 -2 0 0 2 -4 6 5 0 3 5 Hint: the cofactor expansion across the second row is a12 a13 a14 a21 a22 a-23 a24 |AI = a31 a32 a33 a34 a11 a12 a13 a42 a44 a12 a14 a41 a43 a11 a13 a14 a11 a33 a13 a14 a31 a34 + 024 a31 a32 a12 - 23 a32 a34 + a22 a31 a33 a34 a41 a42 a43 a33 a41 a42 a44 = - 021 a32 a41 a.43 a44 a42 a43 a441 93 Using the fact that the matrix is triangular, find its determinant: 0 0 O 2 -2 0 0 A = 6 2 0 4 -8 4 4 1 93 Using the fact that the matrix is triangular, find its determinant: 0 O o o CO 1 O A : -5 -2 NOOOO 0 0 2\f\f\f|E)R% 2 Assume the matrix A is an n X n square matrix. If the equationAx = b has no solution for some b in R\" then A is invertible. O True (O False Given that the coefficient matrix of Ax = 0 is 1 0 1 0 -2 RREF A = 3 2 0 1 4 6 0 0 O -5 This shows that the matrix A has V pivot columns, free variable(s) and is hence V (Hint: free variables give rise to infinitely many solutions to Ax = 0 )