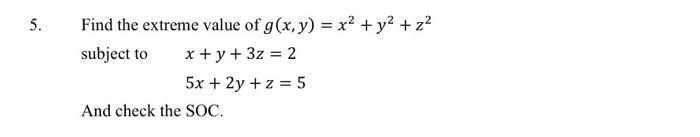
1. 2. 3. Suppose a consumer has a utility function U(x, y) = x0.5y0.5 and faces prices of Px = 4 and Py = 2. The consumer's income is $100. Find the optimal bundle of goods that maximizes the consumer's utility using substitution method? Find the minimum of the function f(x, y) = x + y subject to x + y = 1 using Lagrange multiplier method. Given a function f(x, y, z) = xyz, subject to g(x, y, z) = x + y = 4 and 92(x, y, z) = x + z = 2. a. b. Set up the Lagrange function and find all the F.O.C conditions. (No need to compute the optimal points) Set up the Bordered Hessian matrix. (No need to compute the determinant) 5. Find the extreme value of g(x, y) = x + y + z subject to x + y + 3z = 2 5x + 2y + z = 5 And check the SOC.