1.

2.

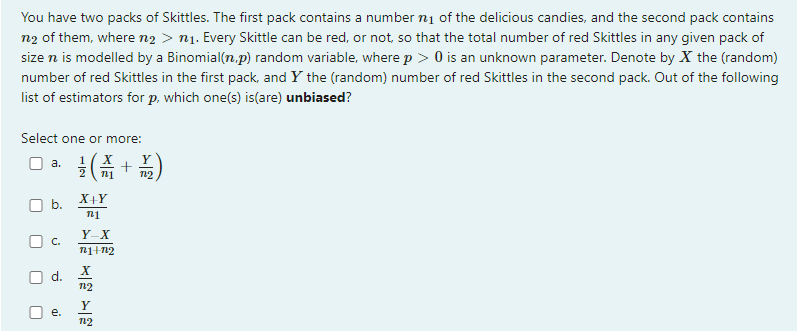
Let n > 3 be an integer. Let y be the present value of a regular annuity (in arrears, payments of 1) for n periods. Let z be the present value of an annuity due (payments of 1) for n periods. Both are computed on the same effective interest rate i > 0. Given this information, which of the following statement(s) is(are) necessarily TRUE (select all which apply)? Select one or more: a. y +1> z b. y+z y d. y + 1 = z e. y + z> n U You have two packs of Skittles. The first pack contains a number of the delicious candies, and the second pack contains n of them, where n>n. Every Skittle can be red, or not, so that the total number of red Skittles in any given pack of size n is modelled by a Binomial(n.p) random variable, where p > 0 is an unknown parameter. Denote by X the (random) number of red Skittles in the first pack, and Y the (random) number of red Skittles in the second pack. Out of the following list of estimators for p, which one(s) is(are) unbiased? Select one or more: U 0 a. C. d. e. Y 1/ ( 1 + 1/2 ) 722 X+Y n1 Y-X n1+n2 K 722 Y 122