Question: 1 Let A -2 3 Find two different diagonal matrices D and the corresponding matrix S such that A = SDS-1. Di = D2

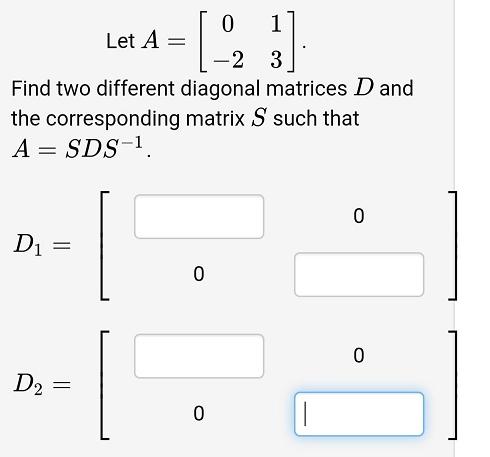
1 Let A -2 3 Find two different diagonal matrices D and

the corresponding matrix S such that A = SDS-1. Di = D2

1 Let A -2 3 Find two different diagonal matrices D and the corresponding matrix S such that A = SDS-1. Di = D2 (2 points) A, P and D are n x n matrices. Check the true statements below: | A. A is diagonalizable if A = PDP-1 for some diagonal matrix D and some invertible matrix P. B. If A is diagonalizable, then A is invertible. C. If there exists a basis for R" consisting entirely of eigenvectors of A, then A is diagonalizable. D. A is diagonalizable if and only if A has n eigenvalues, counting multiplicities.

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Mathematics Questions!

Can two different diagonal matrices be in the same similarity class?

Let A be an invertible diagonalizable n n matrix and let b be an n-column of constant functions. We can solve the system f = Af + b as follows: If g satisfies g = Ag (using Theorem 2), show that f =...

Let D be a nonsingular n Ã n diagonal matrix and let (a) Show that (b) Show that and dmin-min ldil dmax=max ld,il Isisn condi( D) = condoo (D) =-max dmax dmin cond2(D) =

24.3. Asymmetric well potential It is interesting to see what happens when the bosonic potential has two asymmetric wells | a and | b: in this case the asymptotic behaviours of the kink at xare...

Find two different Taylor series to represent the function f(x) = 1/x such that one series is f(x) = a 0 + a 1 (x 1) + a 2 (x 1) 2 + and the other is f(x) = b 0 + b 1 (x 2) + b 3 (x 2) 2 + ...

Show proper workings **For each question, show all workings and have all answers presented in simplest form.** (14) 1. For each pair of functions f(x) and g(x), find (fog) (x) = f(g(x)) and state the...

answer the following questions W Q 4. Let A(x) =1 and (*) =* - What is the value of g( f(-5) ? Round to the nearest hundredth if necessary. O -0.88 O 0.04 O -0.94 O 0.13 W D 5. Describe a series of...

The overall distance traveled by a golf ball is tested by hitting the ball with Iron Byron, a mechanical golfer with a swing that is said to emulate the legendary champion, Byron Nelson. Ten randomly...

Let the joint pmf f(x, y) of X and Y be given by the following: (x, y) f(x, y) (1, 1) ....... 3/8 (2, 1) ....... 1/8 (1, 2) ....... 1/8 (2, 2) ....... 3/8 Find the two conditional probability mass...

Part a The following journal entry was recorded in the books of river limited. Show a detailed explanation of the nature and purpose of this journal entry. DR GST collected 180 DR cash 20 CR GST paid...

A client comes into a bank and requests to make a bank deposit of $9000. Under the Proceeds of Crime and Terrorist Financing Act of 2000 what must the bank do to be compliant with legislation? Select...

In the country Gamma it takes 6 hours to produce one automobile and 1 hour to produce a bale of cotton. In the country Delta it takes 10 hours to produce one automobile and 2.5 hours to produce a...

I. Suppose that there are only 10 individuals in the economy each with the following utility function over present and future consumption : U (c1, c2) = c1 + 2 / 3 c2, where c1 is consumption today,...

QUESTION 10/12 Company A's total royalty expenses for a specific product vary based on the total revenue (dollars in thousand), shown as below: Which of the following statements is correct? 1 point...

The relativistic Doppler shift causes the light from a distant galaxy to be blue shifted by 5%. What is the speed of the galaxy relative to the earth?

Help please:) Engineering Wonders reports net income of $57.0 million. Included in that number is building depreciation expense of $4.7 million and a gain on the sale of land of $1.3 million, Records...

The following data are supplied for the common stocks of Nikola Corporation, Tesla, Inc. and General Motors: Nikola Corp (NKLA) Tesla Inc. (TSLA) Close Price ($) Close Price ($) 67.53 30.00 40.81...

Let A be an m n matrix, V an n r matrix, and B an m r matrix. Show that AX = B if and only if Axj = bj, j = 1,..., r

Let A be a singular n n matrix. Show that ATA is positive semidefinite, but not positive definite.

If A is an n n matrix with the property Ax = 0 for all x Rn, show that A = O.

Calculate the purchase price (flat) of each of the $1000 face value bonds

In the spring of 1992 it became apparent that Olympia & York (O&Y) would have serious difficulty in servicing its debt. Because of this risk, investors were heavily discounting O&Ys bond issues. On...

A $1000, 10% coupon bond issued by Ontario Hydro on July 15, 1994 matures on July 15, 2019. What was its flat price on June 1, 2003 when the required yield to maturity was 5.5% compounded...