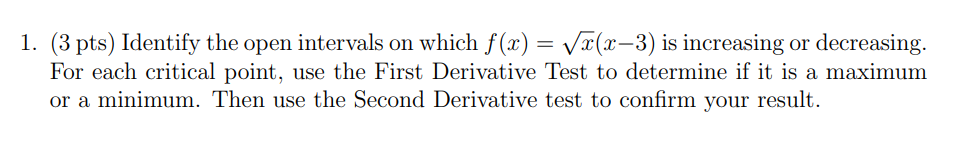
1. (3 pts) Identify the open intervals on which f(x) = \\/z(z3) is increasing or decreasing. For each critical point, use the First Derivative Test to determine if it is a maximum or a minimum. Then use the Second Derivative test to confirm your result. 2. (2 pts) Identify the open intervals on which f(z) = 2* 242 is concave up or concave down. Identify all inflection points. 3. (2 pts) Determine the following limits at infinity. 2x + 1 (a) lim Vx2 + 3 (b) lim cos(x) r-+-co r sin(x) - 1 4. (3 pts) Draw a graph of f(x) with the following properties: . Increasing on (0, co) and Decreasing on (-00, 0) . Concave Up on (-3,5) and Concave Down on (-00, -3) U (5, 00) . lim f(x) = 5 and lim f(x) = 8