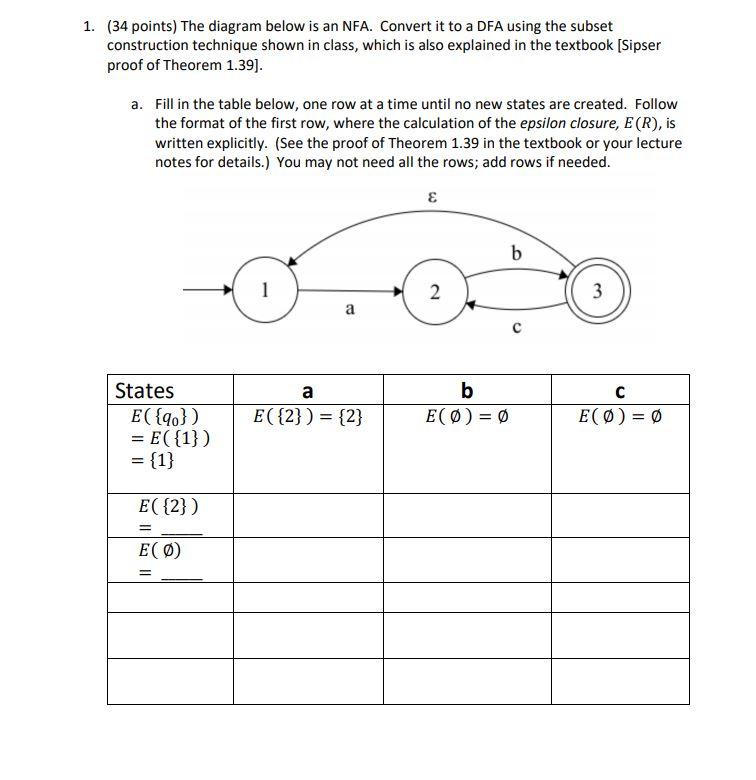
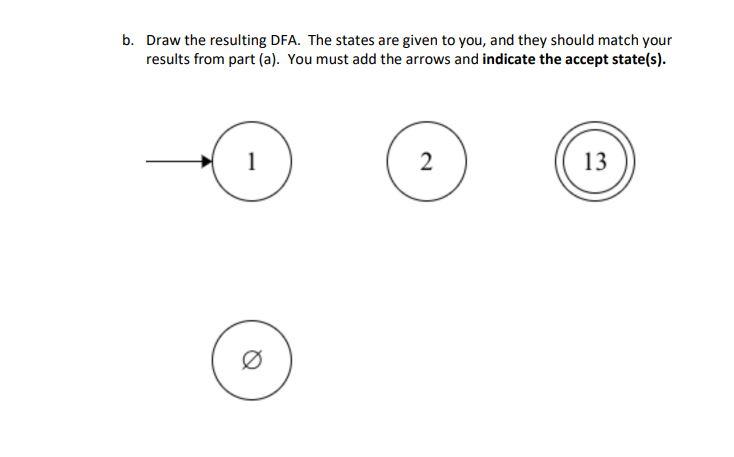
1. (34 points) The diagram below is an NFA. Convert it to a DFA using the subset construction technique shown in class, which is also explained in the textbook (Sipser proof of Theorem 1.39). a. Fill in the table below, one row at a time until no new states are created. Follow the format of the first row, where the calculation of the epsilon closure, E(R), is written explicitly. (See the proof of Theorem 1.39 in the textbook or your lecture notes for details.) You may not need all the rows; add rows if needed. b 2 3 a States E({90}) = E({1}) = {1} a E({2}) = {2} b EO) = 0 E(0) = 0 E({2}) EO) b. Draw the resulting DFA. The states are given to you, and they should match your results from part (a). You must add the arrows and indicate the accept state(s). 1 2 13 C. Test your DFA by listing the set of states it goes through when processing each of the inputs below. Indicate if the DFA accepts or not. (Consider comparing your results to what the given NFA would do, to check your work.) The first one is done for you. Input ab Sequence of DFA states 1, 2, 13 Accepts? Y a ac abc abab abba abcb abcbc