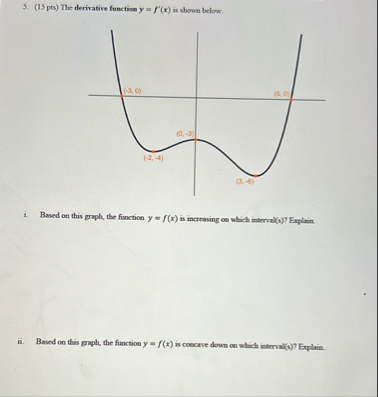
$(15$ pts$)$ The derivative function $y=f^{\text{'}}(x)$ is shown below.

i$.$ Based on this graph, the function $y=f(x)$ is increasing on which morval$($s$)?$ Explain.

ii$.$ Based on this graph, the function $y=f(x)$ is coscave down on which interval$($i$)?$ Explain.$(20$ pts $)$ Below is a graph of the function $y=f(x).$ Assume that all points of discontinuity can be observed from the graph.

Estimate the value for the following nine expressions as accurately as possible based on the graph. Write "DNE" if the value does not exist and $""$ or $"--"$ as appropriate.

$f(3)=$

$\underset{x-6^{-}}{lim}f(x)=$

$\underset{x{2}^{}}{lim}f(x)=$

$\underset{x0}{lim}f(x)=$

$\underset{x3}{lim}f(x)=$

$\frac{df}{dx}{|}_x||=-6=$

$f^{\text{'}}(-4)=$

$\underset{h0}{lim}\frac{f(-1h)-f(-1)}{h}=$

$\underset{x7}{lim}\frac{f(x)-f()}{x-7}=$

Finally, identify all the values $x$ in the interval $(-8,8)$ such that $f$ is ceetimous but not differentiable.$\underset{x0}{lim}\frac{ln(1-x)-sin(x)}{1-co{s}^2(x)}$

a$.$ Using numerical and graphical techniques, we want to find $\underset{x{0}^{-}}{lim}\frac{ln(1-x)-ln(x)}{1-e{m}^2(x)},$ Make sure the mode to your calculator is set to radians.

$\backslash$table$[[x=-0\mathrm{.}1,],[x=-0\mathrm{.}05,\frac{5(1-(-9\mathrm{.}55))-sin(-8\mathrm{.}89)}{1-sin5(-689)}=$ nsuer$],[x=-0\mathrm{.}001,],[x=-0\mathrm{.}0005,]]$

Therefore, by the table above and the graph of the function, the $\underset{x{0}^{}}{lim}\frac{ln(1-x)-sec(x)}{1-co{s}^3(x)},$

b$.$ Using mumerical and graphical techniques, we want to find $\underset{x{0}^{}}{lim}\frac{ln(1-x)-x(x)}{1-co{s}^2(x)}.$

$\backslash$table$[[x=0\mathrm{.}1,],[x=0\mathrm{.}05,],[x=0\mathrm{.}001,],[x=0\mathrm{.}0005,]]$

Therefore, by the table above and the graph of the function, the $\underset{x{0}^2}{lim}\frac{ln(1-x)-sec(x)}{1-co{s}^1(x)}=$

c$.$ Is the function $f(x)=\frac{ln(1-x)-sen(x)}{1-co{s}^2(x)}$ differentiable at $x=0?$ Why or why not?