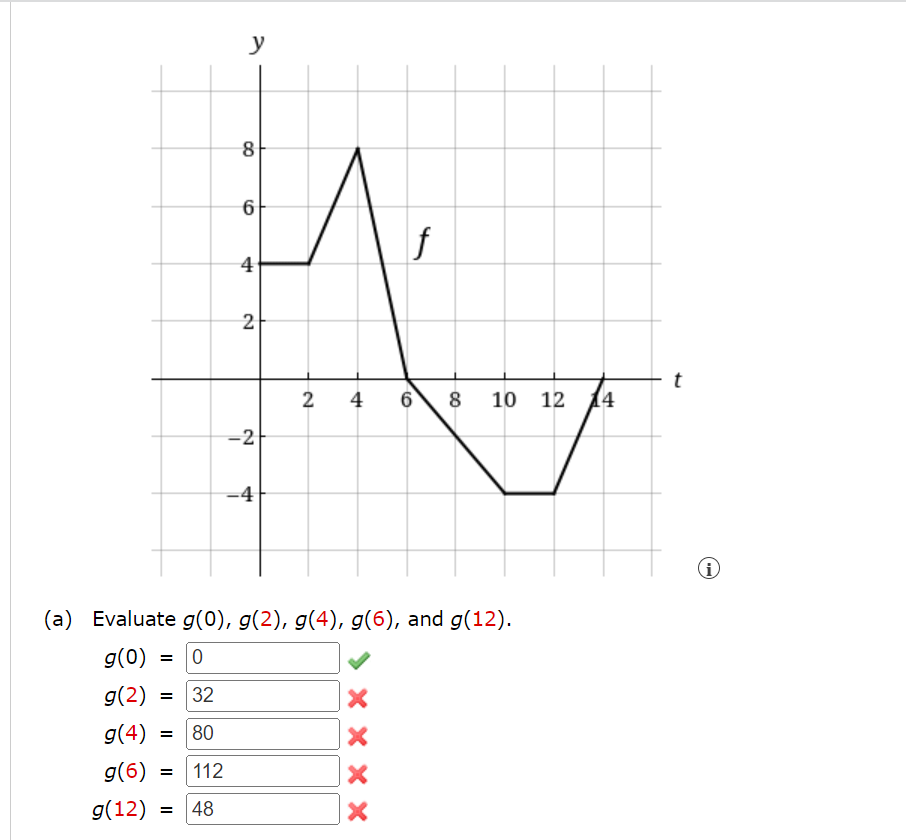
Question: 1. 8- 6 4 2 2 4 6 8 10 12 14 -2 (a) Evaluate g(0), g(2), g(4), g(6), and g(12). 9(0) = 0 g(2)





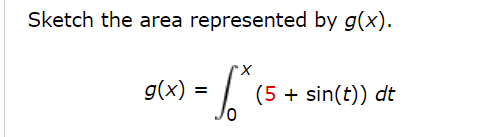

1.
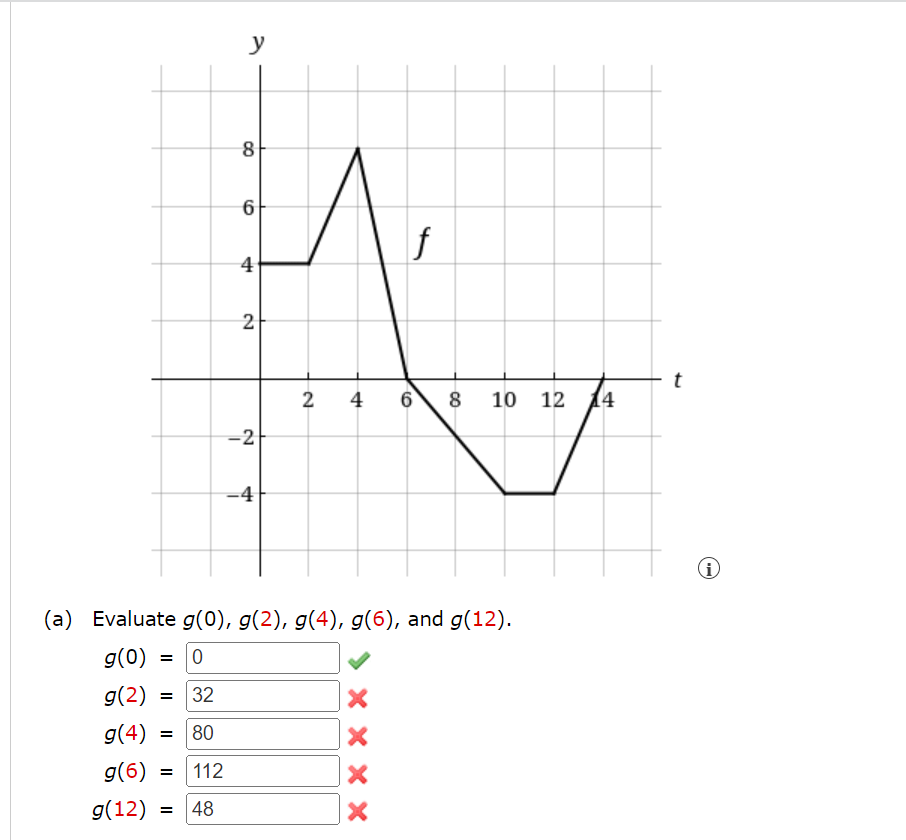



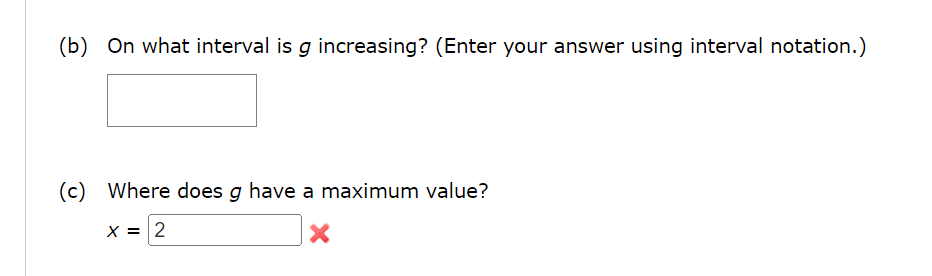


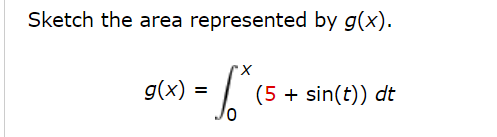

8- 6 4 2 2 4 6 8 10 12 14 -2 (a) Evaluate g(0), g(2), g(4), g(6), and g(12). 9(0) = 0 g(2) = 32 X g(4) = 80 X 9(6) = 112 X g(12) = 48 XUse part one of the fundamental theorem of calculus to find the derivative of the function. 0 0 CX f ( x) = 8 + sec(8t) dt Hint: 8 + sec(8t) dt = - 8 + sec(8t) dt X X o f' ( x ) =Use part one of the Fundamental theorem of calculus to find the derivative of the function. V; 22 MX) = / o'z .. 1 24 + 4 h'(x) = h X Use part one of the Fundamental theorem of calculus to find the derivative of the function. JT/S y= /_ 6 tan(6)d6 .. x/X (b) On what interval is 9 increasing? (Enter your answer using interval notation.) : (c) Where does 9 have a maximum value? X=x \fFind g'(x) in two of the following ways. (a) by using part one of the fundamental theorem of calculus 9'00 = (b) by evaluating the integral using part two of the fundamental theorem of calculus and then differentiating 9'00 = Sketch the area represented by g(x). g ( x ) = (5 + sin(t) ) dt 0Find g'(x) in two of the following ways. (a) by using part one of the fundamental theorem of calculus g'(X) = (b) by evaluating the integral using part two of the fundamental theorem of calculus and then differentiating g'(X) =
Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


