Question: 1 a. Determine whether the Mean Value Theorem applies to the function f(x) = 2x7 on the interval [- 128,128]. b. If so, find or

![function f(x) = 2x7 on the interval [- 128,128]. b. If so,](https://s3.amazonaws.com/si.experts.images/answers/2024/06/6666482160285_169666648212db39.jpg)


![on( 128,128) and is differentiable on [- 128,128]. Therefore, the Mean Value](https://s3.amazonaws.com/si.experts.images/answers/2024/06/66664822a2351_170666648227273f.jpg)

![( 128,128). f(x) is continuous on [- 128,128] and is differentiable on](https://s3.amazonaws.com/si.experts.images/answers/2024/06/66664823c014b_17166664823a4af1.jpg)


![function because f(x) is not continuous on [- 128,128]. b. Select the](https://s3.amazonaws.com/si.experts.images/answers/2024/06/66664824bab3b_172666648249bade.jpg)



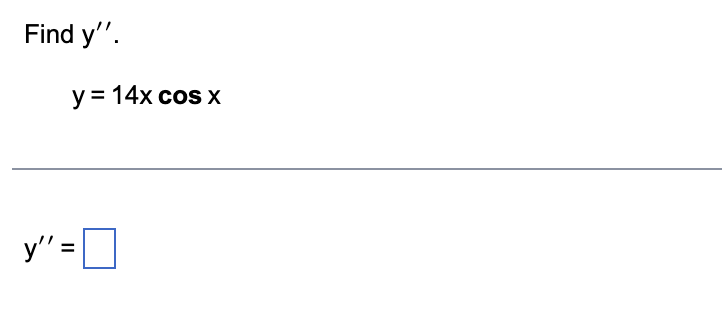
![9x - x on [0,729] . . . What is/are the absolute](https://s3.amazonaws.com/si.experts.images/answers/2024/06/666648275f8d3_1756666482750e1b.jpg)
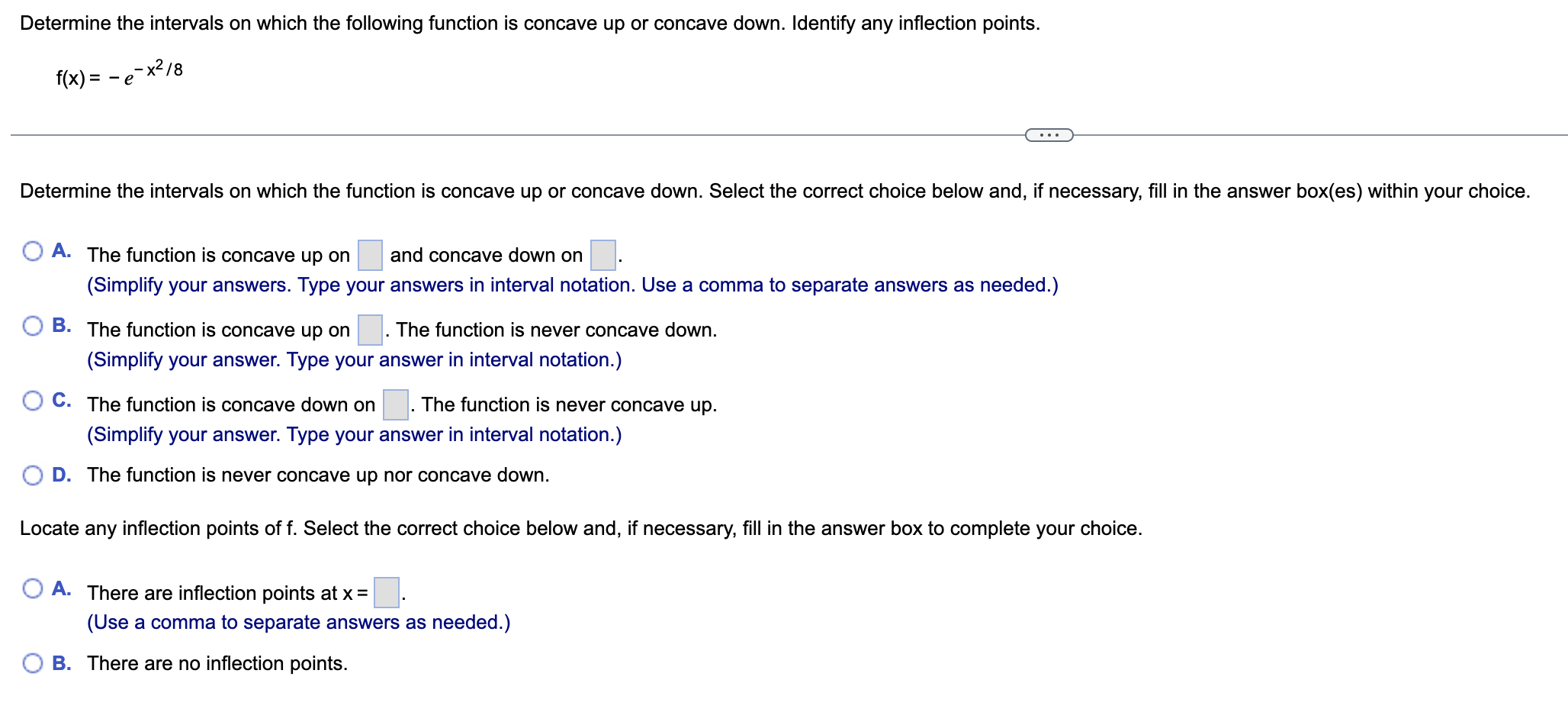
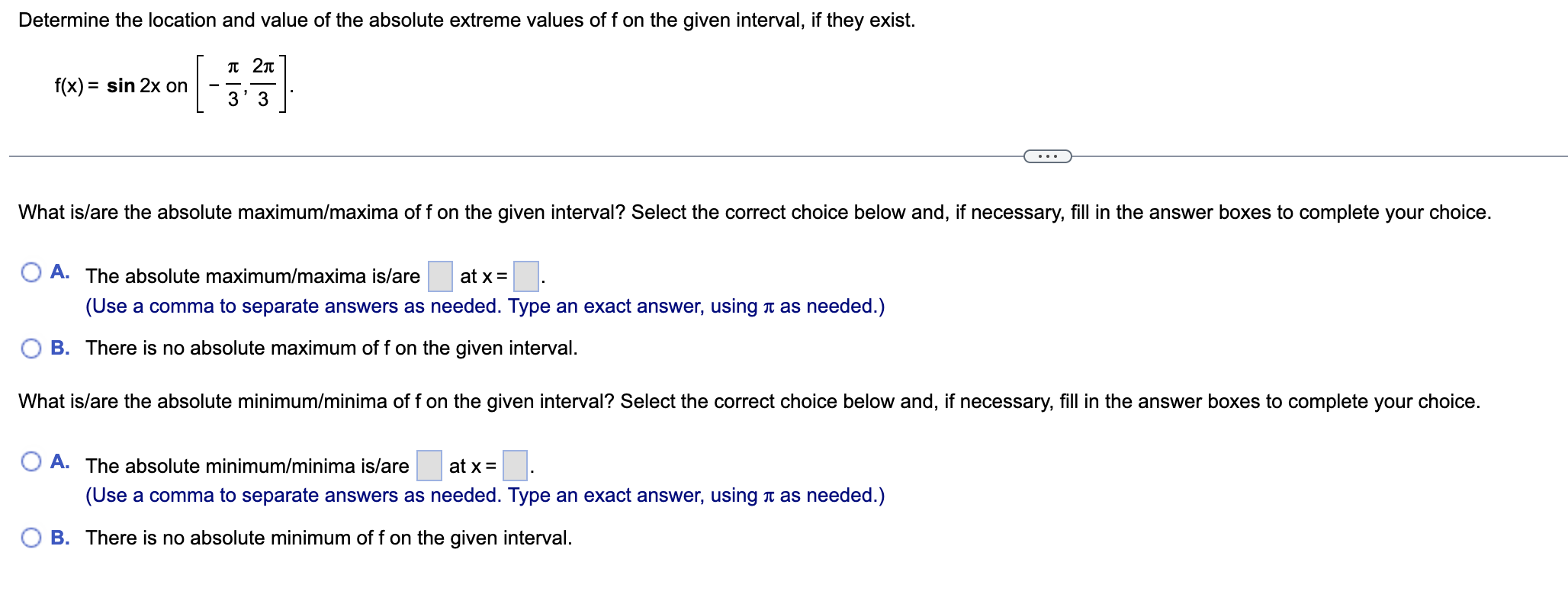
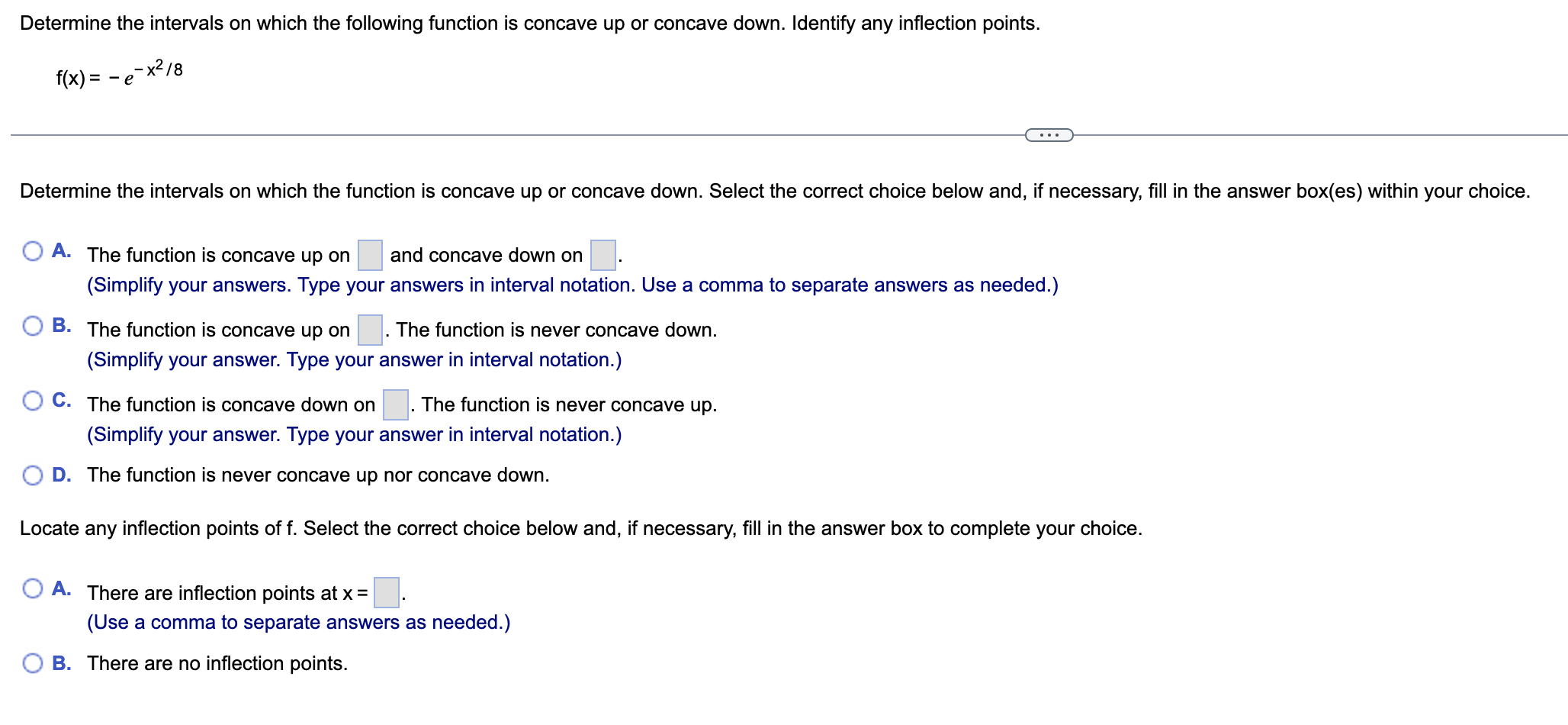
1 a. Determine whether the Mean Value Theorem applies to the function f(x) = 2x7 on the interval [- 128,128]. b. If so, find or approximate the point(s) that are guaranteed to exist by the Mean Value Theorem. 3. Choose the correct answer below. f(x) is continuous on( 128,128) and is differentiable on [- 128,128]. Therefore, the Mean Value Theorem applies to the given function. . The Mean Value Theorem does not apply to the given function because f(x) is not differentiable on ( 128,128). f(x) is continuous on [- 128,128] and is differentiable on ( 128,128). Therefore, the Mean Value Theorem applies to the given function. 6558;; . The Mean Value Theorem does not apply to the given function because f(x) is not continuous on [- 128,128]. b. Select the correct choice below and, if necessary, fill in the answer box to complete your choice. ":3 A- The point(s) islare x= (Type exponential notation with positive exponents. Use integers or fractions for any numbers in the expression.) {:2- B. The Mean Value Theorem does not apply in this case. Determine the location and value of the absolute extreme values of f on the given interval, if they exist. " WIN f(x) = 9x - x on [0,729] . . . What is/are the absolute maximum/maxima of f on the given interval? Select the correct choice below and, if necessary, fill in the answer boxes to complete your choice. O A. The absolute maximum/maxima is/are at X = (Use a comma to separate answers as needed.) O B. There is no absolute maximum of f on the given interval. What is/are the absolute minimum/minima of f on the given interval? Select the correct choice below and, if necessary, fill in the answer boxes to complete your choice. O A. The absolute minimum/minima is/are at x = (Use a comma to separate answers as needed.) O B. There is no absolute minimum of f on the given interval.Use the derivative f' to determine the local minima and maxima offand the intervals of increase and decrease. Sketch a possible graph of f (f is not unique). f'(x) = 2 sin 2x on [- 21:21:] The local minimum/minima is/are at x= |_|. (Use a comma to separate answers as needed. Type an exact answer, using 1: as needed.) The local maximum/maxima is/are at x = (Use a comma to separate answers as needed. Type an exact answer, using 1: as needed.) Find the intervals of increase and decrease of f. Choose the correct answer below. Ci . . . 31: 1: 1: 31: flsmcreaslngon -21:,-? , -1:,-E , 0,5 ,and 1m? . . . 31: 1: 1: 31: flsdecreasmgon - 2 ,-1:, -2,0, 2,1: ,and 2 ,21:. Cl I I 31: 1: 1: 31: flsdecreasmgon -21:,- 2 , 1:,-2 , 0,2 ,and 1:2 . . . . 31: 1: 1: 31: flsmcreaslngon - 2 ,-1:, -2,0, 2,1: ,and 2 ,21:. Sketch a possible graph of f. Choose the correct graph below. Q B. {'j' c. C D. Compute the following derivative using the method of your choice. (axe + 97x) Determine the location and value of the absolute extreme values of f on the given interval, if they exist. f(x) = sin 2x on 3 ' 3 . . . What is/are the absolute maximum/maxima of f on the given interval? Select the correct choice below and, if necessary, fill in the answer boxes to complete your choice. O A. The absolute maximum/maxima is/are at X = (Use a comma to separate answers as needed. Type an exact answer, using it as needed.) O B. There is no absolute maximum of f on the given interval. What is/are the absolute minimum/minima of f on the given interval? Select the correct choice below and, if necessary, fill in the answer boxes to complete your choice. O A. The absolute minimum/minima is/are at X = (Use a comma to separate answers as needed. Type an exact answer, using it as needed.) O B. There is no absolute minimum of f on the given interval.Determine the intervals on which the following function is concave up or concave down. Identify any inflection points. f(x) = - e- x2 /8 . . . Determine the intervals on which the function is concave up or concave down. Select the correct choice below and, if necessary, fill in the answer box(es) within your choice. O A. The function is concave up on and concave down on (Simplify your answers. Type your answers in interval notation. Use a comma to separate answers as needed.) O B. The function is concave up on . The function is never concave down. (Simplify your answer. Type your answer in interval notation.) O C. The function is concave down on . The function is never concave up. (Simplify your answer. Type your answer in interval notation.) O D. The function is never concave up nor concave down. Locate any inflection points of f. Select the correct choice below and, if necessary, fill in the answer box to complete your choice. O A. There are inflection points at x = (Use a comma to separate answers as needed.) O B. There are no inflection points.A swimming pool is 50 m long and 20 m wide. Its depth decreases linearly along the length from 3 m to 1 m. It is initially empty and is filled at a rate of 1 m/min. How fast is the water Inflow 1 m /min level rising 360 min after the filling begins? How long will it take to fill the pool? 50 m- 1 m 20 m 3 m Let V, h, and w be the volume, depth, and width of the pool, respectively. Write an equation relating V and h at 360 min after the filling begins. Differentiate both sides of the equation with respect to t. dV dh dt The water is rising at a rate of 360 min after the filling begins. (Simplify your answer.) It will take |minutes to fill the pool.Find y". y = 14x cos x y'=
Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


