Question: 1. A sequence {Pn} converges superlinearly if: Pn+1 - P lim 0 n Pn - P Suppose that {n} converges superlinearly to p. Show:

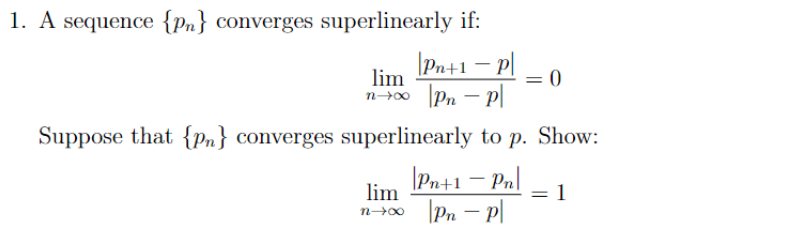
1. A sequence {Pn} converges superlinearly if: Pn+1 - P lim 0 n Pn - P Suppose that {n} converges superlinearly to p. Show: lim |Pn+1 - Pn = 1 n |Pn - P

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock

Let pn be a sequence that converges superlinearly to p ie lim Po1... View full answer

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Mathematics Questions!

Self-Reflection Question 1 : Have you been a caregiver for your own family or observed caregiving experiences among your family and friends? Reflect on how these experiences have influenced your...

The new line character is utilized solely as the last person in each message. On association with the server, a client can possibly (I) question the situation with a client by sending the client's...

Developments in Technology Light is incident from air on the end face of a multimode optical fibre at angle of incidence as shown below. n n 1 2 The refractive indices of the core and cladding are...

Show work/explanation where indicated. Answers without any work may earn little, if any, credit. You may type or write your work in your copy of the exam, or if you prefer, create a document...

Recall that N is the set of positive integers and Q is the set of rational numbers. NOTE: "Limit point\Sequences - Part 2 (Week 4) Infinite Limits Definition. A sequence (sn) is said to diverge to +...

1. (60 pts True/False. Indicate whether the statement is true or false. If the statement is false, present an explanation or counterexample. (No explanation necessary for each true statement.) (2...

Sections 10.1 and 10.2 Reading Assignment: Sequences and Series Answer Only Exercise 1, 2, and 3 by using a screenshot provided Calculus Pearson textbook. Make sure you read these three questions...

# 5: Fourier Interpolant and DFT 1 The Discrete Fourier Transform (DFT) of a periodic array fj , for j = 0, 1, . . . , N 1 (corresponding to data at equally spaced points, starting at the left end...

. The speed at which the sequence generated by an iterative method converges is called the methods ORDER of convergence. There are many types of orders of convergence: linear, su- perlinear,...

For the circuit shown in the figure, the Mesh Equation for loop 1 is: 3 1 2 ww iz i 2V 2 6V i4 4V iz 4 10 5 V Select one: O a. 1011-5l2-6l3=2 O b. 511-912+313=6 O c. 1011-512-213=2 O d....

Wong Corporation reports the following beginning inventory and inventory purchases, Inventory balance at beginning of year Inventory purchased during the year. Cost of goods available for sale during...

5 Work out the first three terms and the 8th term of the sequences with the given nth term. 1 1 4m a d 2.5n-0.4 C 6+1.75 11+31 b 2 2 2

Two-point charges +Q and +4Q are placed at a distance a apart on a horizontal plane. Where should the third charge be placed for it to be in equilibrium?

Choose the correct answer: 1. The plan _______ ten minutes ago. landed land lands 2. John _______ ill yesterday. was is am 3. She _______ when I told her the joke. laugh laughed laughs 4. My friend...

Choose the correct word: 1. We usually _______ lunch at the school. has have did 2. The weather _______ beautiful today. is am will 3. Summer often _______ sandwiches for lunch. has will am 4. Tom...

Explain to me how to calculate average annual growth rate please? In 1960Q3, real GDP per capital was $17,223. In 2017Q3, real GDP was per capita $52,605. What was the average annual growth rate over...

2. Use the strangeness law to show that the following reactions are not allowed: a) n+p - 30 + KO + no b) 1 + n - p + p + 3n + + 3n c) p + P - p + n o + A0 + K -

Use the LaPlace transform t o solve the given initial value problem. y ' ' - 4 y ' + 4 y = 3 t 2 e 2 t , y ( 0 ) = 0 , y ' ( 0 ) = 4

Suppose that an electronic system contains n components that function independently of each other, and suppose that these components are connected in series, as defined in Exercise 5 of Sec. 3.7....

Consider again the problem described in Exercise 6, and assume the same prior distribution of . Suppose now, however, that instead of selecting a random sample of eight items from the lot, we perform...

Suppose that a random variable X has a continuous distribution for which the p.d.f. is as follows: Determine all the medians of this distribution. f(x)lorx > 0, 0 otherwise. for >

Forrester owns a nonrental business with two separate departments. Department A generates net income of $70,000, and Department B generates a net loss of $58,000. Forrester participates 800 hours in...

Ann and Bill were on the list of a local adoption agency for several years seeking to adopt a child. Finally, in 2015, good news comes their way and an adoption seems imminent. They pay qualified...

Dorothy acquired a 100% interest in two passive activities: Activity A in January 2011 and Activity B in 2012. Through 2014, Activity A was profitable, but it produced losses of $200,000 in 2015 and...