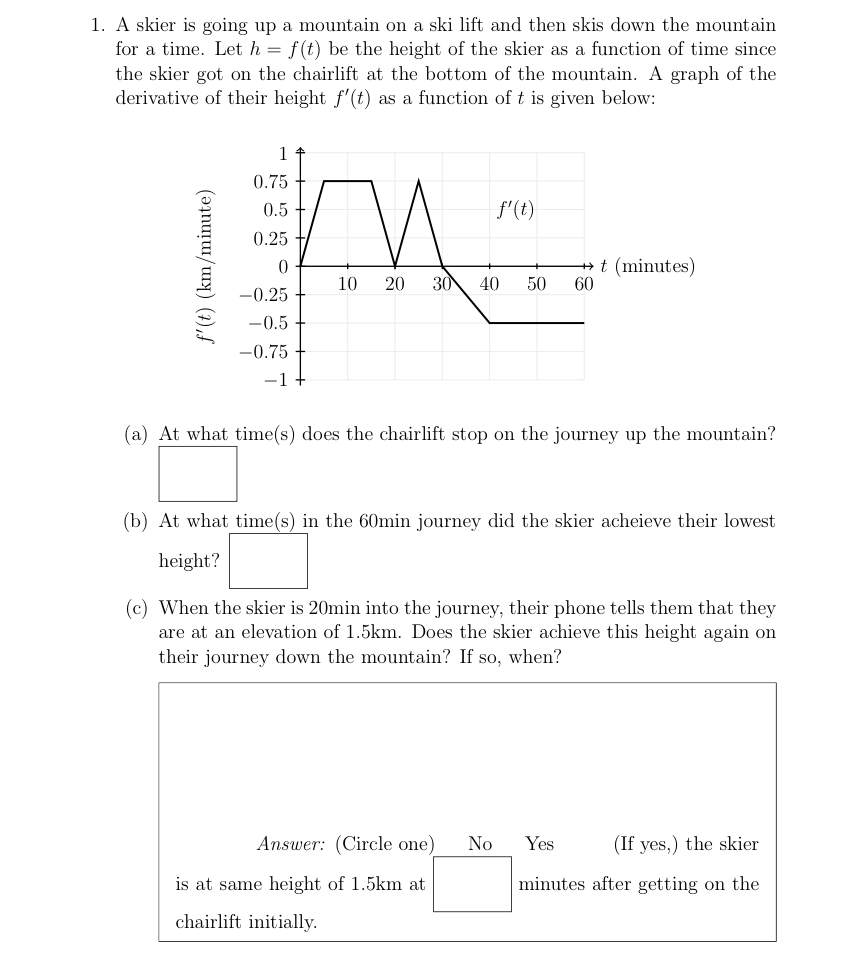
1. A skier is going up a mountain on a ski lift and then skis down the mountain for a time. Let h= f(t) be the height of the skier as a function of time since the skier got on the chairlift at the bottom of the mountain. A graph of the derivative of their height f'(t) as a function of t is given below: f'(t) (km/minute) 1 0.75 0.5 0.25 0 -0.25 -0.5 -0.75 M 10 20 30 f'(t) 40 (a) At what time(s) does the chairlift stop on the journey up the mountain? t (minutes) 50 60 (b) At what time(s) in the 60min journey did the skier acheieve their lowest height? Answer: (Circle one) No is at same height of 1.5km at chairlift initially. (c) When the skier is 20min into the journey, their phone tells them that they are at an elevation of 1.5km. Does the skier achieve this height again on their journey down the mountain? If so, when? Yes (If yes,) the skier minutes after getting on the