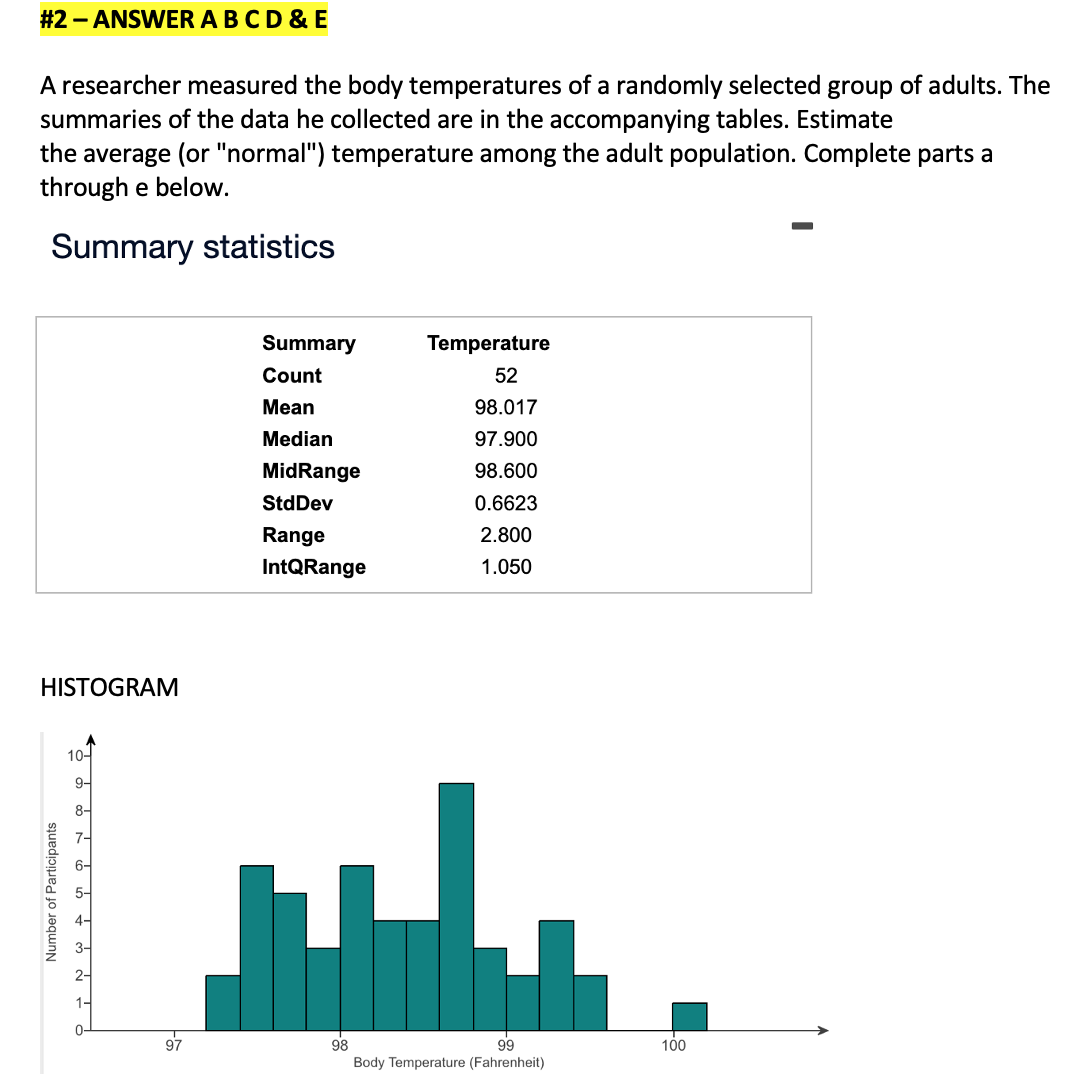
#1 - ANSWER A B 8: C. A scientist measured the speed of light. His values are in km/sec and have 299,000 subtracted from them. He reported the results of 20 trials with a mean of 756.22 and a standard deviation of 118.91. a) Find a 90% confidence interval for the true speed of light from these statistics. b) State in words what this interval means. Keep in mind that the speed of light is a physical constant that, as far as we know, has a value that is true throughout the universe. c) What assumptions must you make in order to use your method? 4: .1 4b 3) A90% condence interval for the true speed of light is (D km/sec, D km/sec). (Round to two decimal places as needed.) 4' b) In words, what does the 90% confidence interval mean? A. For all samples, 90% of them will have a mean speed of light that falls within the confidence interval. B. The confidence interval contains the true speed of light 90% of the time. C. With 90% confidence. based on these data, the speed of light is between the lower and upper bounds of the confidence interval. D. Any measurement of the speed of light will fall within this interval 90% of the time. 4 c) What assumptions must you make in order to use your method? Select all that apply. A. The measurements are independent. B. The measurements arise from a random sample or suitably randomized experiment. C. The sample is drawn from a large population. D. The data come from a distribution that is nearly normal. E. The data come from a distribution that is nearly uniform. #2 - ANSWER A B C D & E A researcher measured the body temperatures of a randomly selected group of adults. The summaries of the data he collected are in the accompanying tables. Estimate the average (or "normal") temperature among the adult population. Complete parts a through e below. Summary statistics Summary Temperature Count 52 Mean 98.017 Median 97.900 MidRange 98.600 StdDev 0.6623 Range 2.800 IntQRange 1.050 HISTOGRAM Number of Participants 97 98 99 100 Body Temperature (Fahrenheit)a) Check the conditions for creating a t-interval. Which condition(s) is(are) met? Select all that apply. A. 10% Condition B. Nearly Normal Condition C. Randomization Condition >b) Find a 90% confidence interval for the mean body temperature. The needed t* value is 1.675. The 90% confidence interval for the mean body temperature is (Round to two decimal places as needed.)> c) Explain the meaning of the interval. Choose the correct answer below. O A. There is 90% confidence, based on the data, that the interval contains the mean body temperature. O B. There is 90% confidence, based on the data, that the body temperature for all adults falls in the interval. O C. There is 90% confidence, based on the data, that the mean body temperature will always fall in the interval. O D. There is 90% confidence, based on the data, that the body temperature for an adult falls in the interval. >d) Explain what "90% confidence" means in this context. Choose the correct answer below. O A. 90% of all adults have body temperatures that fall in the interval. O B. 90% of all samples of size 52 have a mean body temperature that is in the interval. O C. 90% of all such random samples will produce intervals containing the true mean temperature. O D. 90% of all adults sampled have body temperatures that fall in the interval. e) A temperature of 98.6 F is commonly assumed to be "normal." Do these data suggest otherwise? Explain. Since the 90% confidence interval contains, does not contain (choose the correct answer) the "normal" temperature, the data suggest that a temperature of 98.6 F is plausible, not plausible (choose the correct answer)