#1) Answer full question (a-f), showing work for thumbs up

Suppose X be a continuous random variable with uniform distribution, X Unif (1, 2), and given X = x, Y is an exponential with parameter = .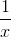

Hint: Use the law of total expectation (tower rule)

(a) Compute the blind estimate of X.

(b) Find the best linear estimate of X given Y.

(c) Find the mean square error (MSE) of this estimator.

(d) Let 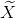= X 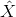_L(Y ) be the error of the estimation. Compute E[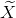Y ].

(e) Find the MMSE estimator of X given Y = y.

(f) What the average estimation error for the estimator of (e)?

Suppose X be a continuous random variable with uniform distribution, X ~ Unif(1, 2), and given X = X, Y is an exponential with parameter 1 = 1 Hint: Use the law of total expectation (tower rule). (a) Compute the blind estimate of X. (b) Find the best linear estimate of X given Y. (c) Find the mean square error (MSE) of this estimator. (d) Let = X L(Y) be the error of the estimation. Compute E(XY). (e) Find the MMSE estimator of X given Y = y. (f) What the average estimation error for the estimator of (e)? 2 X Suppose X be a continuous random variable with uniform distribution, X ~ Unif(1, 2), and given X = X, Y is an exponential with parameter 1 = 1 Hint: Use the law of total expectation (tower rule). (a) Compute the blind estimate of X. (b) Find the best linear estimate of X given Y. (c) Find the mean square error (MSE) of this estimator. (d) Let = X L(Y) be the error of the estimation. Compute E(XY). (e) Find the MMSE estimator of X given Y = y. (f) What the average estimation error for the estimator of (e)? 2 X