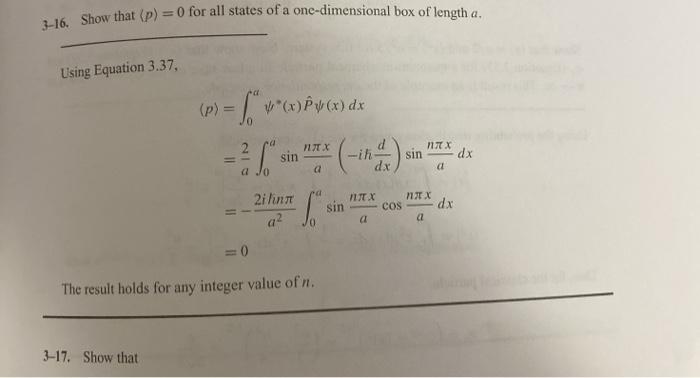
1) Calculate (p2) 2) Use the result from problem #1 above and problems 3-16 and 3-17 to show that OxOp >for a particle in a one-dimensional box. 3-16. Show that (P) = 0 for all states of a one-dimensional box of length a. Using Equation 3.37, (N="d . TX sin sin a dx a dx 2ilung a2 TX dx TX COS a sin The result holds for any integer value of n. 3-17. Show that for a particle in a box is less than a, the width of the box, for any value of n. Ifo, is the uncertainty in the position of the particle, could o, ever be larger than a? Chapter 3 0,= ((x2) - ()31/2 From the solutions to Problems B-8 and B-9 (or Equations 3.31 and 3.32 in the text), (x ) = al a2 3 42 2n2112 Then, as detailed in Problems B-9 and B-10, 1/2 a a2 2n272 1/2 =a 1 12 2nfa2 2n212