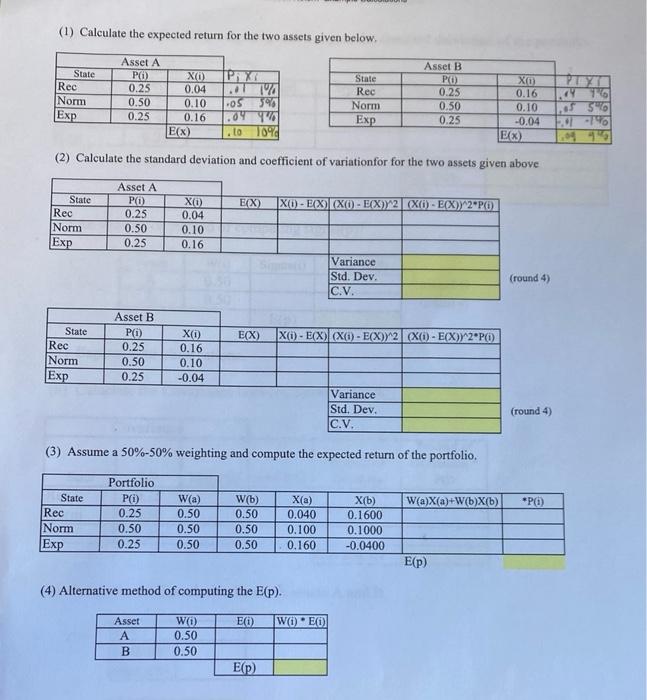
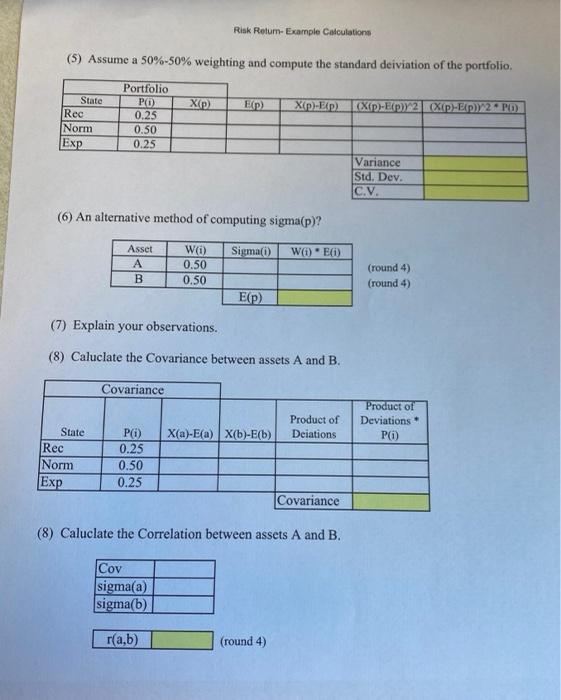
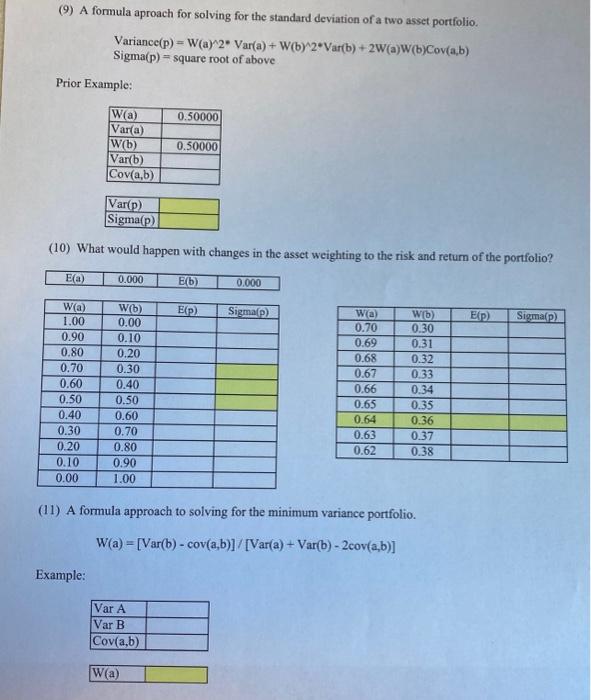
(1) Calculate the expected return for the two assets given below. State Rec Norm Exp Asset A P(i) 0.25 0.50 0.25 XO 0.04 0.10 0.16 EX) ..11 os 599 .04 TO .L01094 State Rec Norm Exp Asset B ) 0.25 0.50 0.25 ) 0.16 0.10 -0.04 EX) Y TO 50 -7% (2) Calculate the standard deviation and coefficient of variationfor for the two assets given above EX) XO - E(X) (XO - E(X)/2 X(i) - E(X)/2"PO) State Rec Norm Exp Asset A Pi) 0.25 0.50 0.25 X1) 0.04 0.10 0.16 Variance Std. Dev. C.V. (round 4) E(X) X) - E(X)(x(i) - E(X)) 2 (Xi) - E(X)/2*PO State Rec Norm Exp Asset B Pi) 0.25 0.50 0.25 Xo 0.16 0.10 -0.04 Variance Std. Dev. C.V. (round 4) (3) Assume a 50%-50% weighting and compute the expected return of the portfolio. W(a)X(a) W(b)X(b) *P1) State Rec Norm Exp Portfolio Pi) 0.25 0.50 0.25 W(a) 0.50 0.50 0.50 Wb) 0.50 0.50 0.50 X(a) 0.040 0.100 0.160 X(b) 0.1600 0.1000 -0.0400 E(P) (4) Alternative method of computing the E(p). EO) WEO) Asset B WO 0.50 0.50 E(p) Risk Retum- Example Calculations (5) Assume a 50%-50% weighting and compute the standard deviation of the portfolio X(p) E(P) X{p)-EP) KXp)-ExpY2Xp.- EY 2. PO State Rec Norm Exp Portfolio PD) 0.25 0.50 0.25 Variance Std. Dev. C.V. (6) An alternative method of computing sigma(p)? Sigma(i) W()E) Asset A B W() 0.50 0.50 (round 4) (round 4) E() (7) Explain your observations. (8) Caluclate the Covariance between assets A and B. Covariance Product of Deviations P() Product of Deiations X(a)-Ea) X(b)-E(b) State Rec Norm Exp Pi) 0.25 0.50 0.25 Covariance (8) Caluclate the correlation between assets A and B. Cov sigma(a) sigma(b) r(a,b) (round 4) (9) A formula aproach for solving for the standard deviation of a two asset portfolio. Variance(p) = Way 2. Var(a) + W(by2Vartb) + 2W(a)W(b)Cov(a,b) Sigma(p) = square root of above Prior Example: 0.50000 Wa) Var(a) W(b) Var(b) Cov(a,b) 0.50000 Var(p) Sigma(p) (10) What would happen with changes in the asset weighting to the risk and return of the portfolio? Ea) 0.000 E(b) 0.000 EP) Sigmap) E{p) Sigmap) W(a) 1.00 0.90 0.80 0.70 0.60 0.50 0.40 0.30 0.20 0.10 0.00 W) 0.00 0.10 0.20 0.30 0.40 0.50 0.60 0.70 0.80 0.90 1.00 Wa) 0.70 0.69 0.68 0.67 0.66 0.65 0.64 0.63 0.62 Wb) 0.30 0.31 0.32 0.33 0.34 0.35 0.36 0.37 0.38 (11) A formula approach to solving for the minimum variance portfolio. W(a) [Var(b) - cov(a,b)]/[Var(a) + Var(b) - 2cov(a,b)] Example: Var A Var B Cov(a,b) W(a)