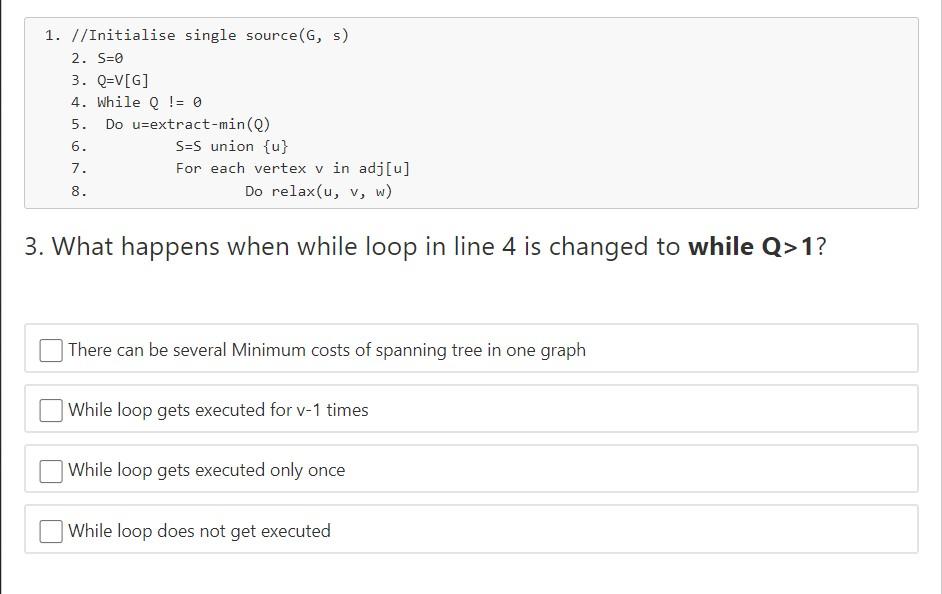
1. Can we perform maximum spanning tree using "Kruskal" ? Give Proper explanation in PDF Yes, It can be done by modifying the weight values Yes, It can be done by modifying the direction of the edges No, it is not possible. Yes, It can be done by using max-heap or sorting the edge weights with decreasing order 1. //Initialise single source(G, ) 2. S=0 3. Q=V[G] 4. While Q != 0 5. Do u=extract-min(Q) 6. SES union {u} 7. For each vertex v in adj[u] 8. Do relax(u, v, W) 3. What happens when while loop in line 4 is changed to while Q>1? There can be several Minimum costs of spanning tree in one graph While loop gets executed for v-1 times While loop gets executed only once While loop does not get executed 2. Which of the following is/are not false? Prims' never accepts cycles in the MST There can be several Minimum costs of spanning tree in one graph Complexity of Dijstra algorithm can be (V*V) Kruskal can work in weighted directed sparse graph Weighted interval scheduling requires Dynamic programming SCC means Shortest connected components Prim's algorithm initialises with a vertex which has smallest edge