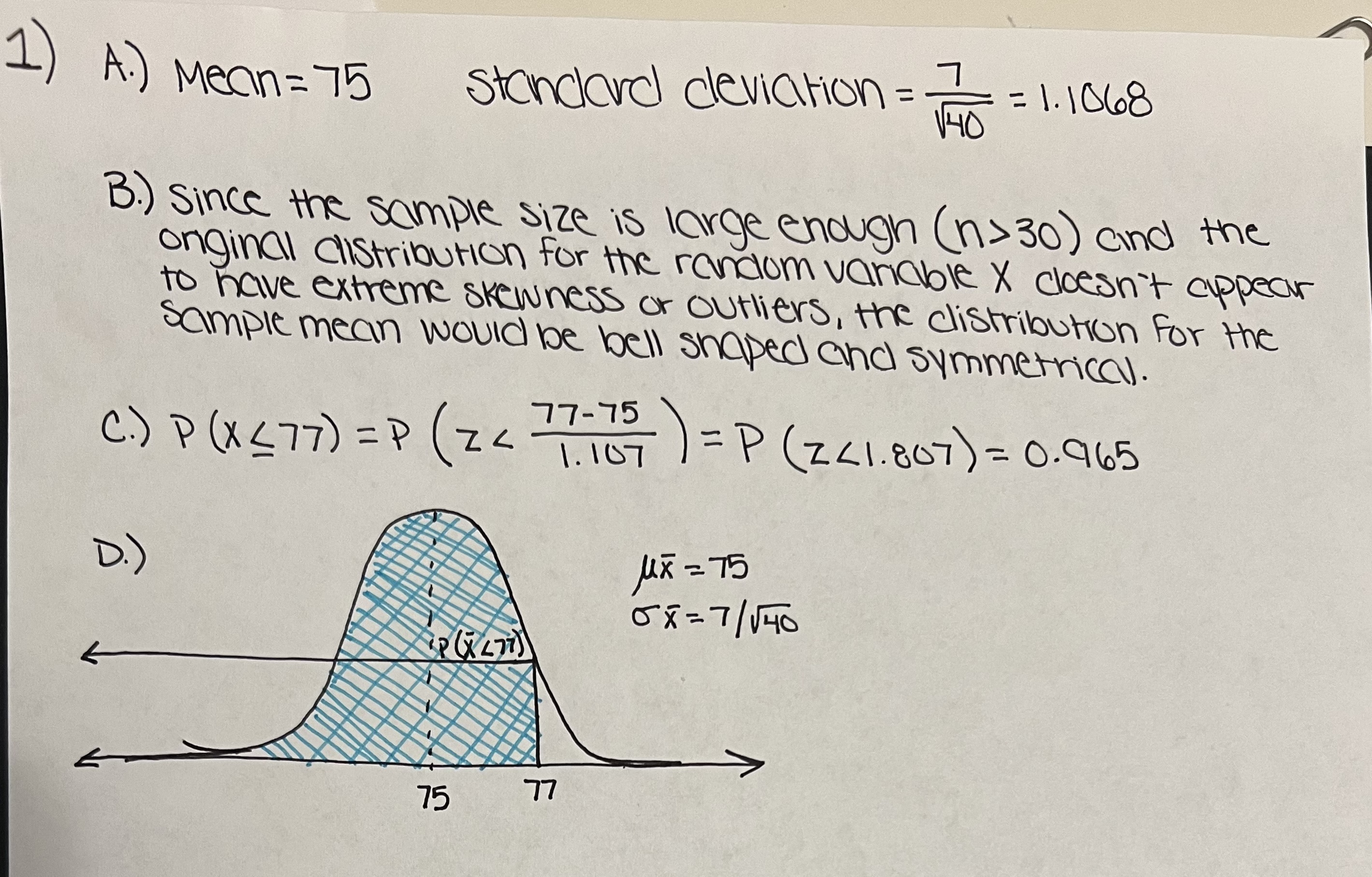
1. Consider a parent population with mean 75 and a standard deviation 7. The population doesn't appear to have extreme skewness or outliers. A. What are the mean and standard deviation of the distribution of sample means for n = 40? (2 points) B. What's the shape of the distribution? Explain your answer in terms of the Central Limit Theorem. (1 point) C. What proportion of the sample means of size 40 would you expect to be 77 or less? If you use your calculator, show what you entered. (1 point) D. Draw a sketch of the probability you found in part C. (1 point) 1) A.) Mean = 75 standard deviation = 17/05 = 1.1068 - 0 B.) Since the sample size is large enough (n>30) and the onginal distribution for the random vaable X cloesn't appear to have extreme skewness or outliers, the distribution for the Sample mean would be bell shaped and symmetrical. C.) P (X 77) =P (z < 7-7597) = P (241.807) = 0.965 D.) P(277) 1.107 = M 275 58=7/40 75 77