Question: 1. Consider $left[begin{array}{rr}1 & -3 12 & 6 7 & -3 3& 4end{array} ight]left[begin{array}{1}x_{1} x_{2} end{array} ight] equivleft[begin{array}{1}1 3 2 1 end{array} ight]$ Find

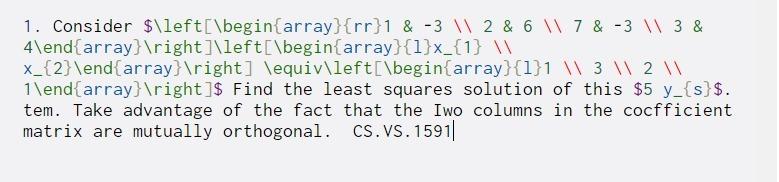
$1. Consider $\left[\begin{array}{rr}1 & -3 12 & 6 7 & -3$

1. Consider $\left[\begin{array}{rr}1 & -3 12 & 6 7 & -3 3& 4\end{array} ight]\left[\begin{array}{1}x_{1} \ x_{2} \end{array} ight] \equiv\left[\begin{array}{1}1 3 2 1 \end{array} ight]$ Find the least squares solution of this $5 y_{s}$. tem. Take advantage of the fact that the Iwo columns in the cocfficient matrix are mutually orthogonal. CS.VS. 1591||

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Databases Questions!

1. Consider $\left[\begin{array}{rr}1 & -3 2 & 6 7 & -3 3& 4\end{array} ight]\left[\begin{array}{1}x_{1} \ x_{2} \end{array} ight] \equiv\left[\begin{array}{1}1 3 2 1 1\end{array} ight]$ Find the...

1. Find the 5 th roots of $\frac{(-1-\sqrt{3} i)^{2021}}{(- \sqrt{3}+i)^{3}(-2+2 i)^{12}}$ and plot them in the complex plane 2. Consider the linear system $$ \left(\begin{array}{1111} 1 & 1 & 1 & 2...

Math\t107-6381\t-\tQuiz\t#4\t-\tSchultz\t-\tDue\tFebruary\t21,\t2016\t-\tpage\t1\tof 3 Follow\tthese\tdirections\tcarefully. This\tquiz\tis\tdue\tby\t11:59\tEastern\ttime\ton\tFebruary\t21,\t2016. o...

seventh pages Chapter 3 Curve Sketching How much metal would be required to make a 400-mL soup can? What is the least amount of cardboard needed to build a box that holds 3000 cm3 of cereal? The...

Probability and Statistics - Problem Set c Keith M. Chugg October 2, 2015 1 Preliminaries, Combinatorics, Set Probability 1.1. A number of bats are in a cave. 2 bats can see out of their left eye. 3...

Least Squares Approximation Hector D. Ceniceros 1 Least Squares Approximation Let f be a continuous function on [a, b]. We would like to find the best approximation to f by a polynomial of degree at...

Code the function greedy_predicator without using numpy/pandas Please include explanation of the code & the computational complexity To see the description of the function: Scroll down the...

Set Student Name: 1. Describe the relationship between two variables that have a correlation coefficient value: a. Near -1 b. Near 0 c. Near 1 2. Data was collected where a weightlifter was asked to...

Consider the Initial Value Problem: $$ \begin{array}{111} x_{1}^{\prime} & =6 x_{1}+3 x_{2} & x_{1}(0) & =8 x_{2}^{\prime} & =-15 x_{1}-6 x_{2}, & x_{2}(0) & = 7 \end{array} $$ (a) Find the...

Instuctor's Annotated Edition TENTH EDITION Understandable Statistics Concepts and Methods Charles Henry Brase Regis University Corrinne Pellillo Brase Arapahoe Community College Australia Brazil...

Denver is a supervisory employee of Atlantis Corporation. He had the following items of gross income during the year Denver was paid P800,000 salaries Denver's P100,000 personal loan was paid by...

In its February 21 19981 issue. Fortune magazine published the results of a Yankelovich partners survey of 600 adults that investigated their ideas about marriage1 divorce1 and the contributions of...

9 All else held constant, which one of the following actions is most likely to increase the WACC of a levered firm? Multiple Choice An increase in the weight of debt A decrease in a firm's equity...

Compared with half a century ago, adoption has become _ _ _ _ _ _ _ _ _ common, but it is more open and acceptabl e , so we probably discuss it _ _ _ _ _ _ _ . fill in the blanks more or much less or...

9. What are some potential advantages and disadvantages of attitude-awareness-based diversity training programs?

6. The director of sales and marketing for a Warner Brothers theme park has been working in Madrid. She is getting ready to return to the United States. What should Warner Brothers do to ensure her...

11. List and discuss the steps involved in developing a succession planning system. How might a succession planning system differ between high-potential employees and employees with midlevel...