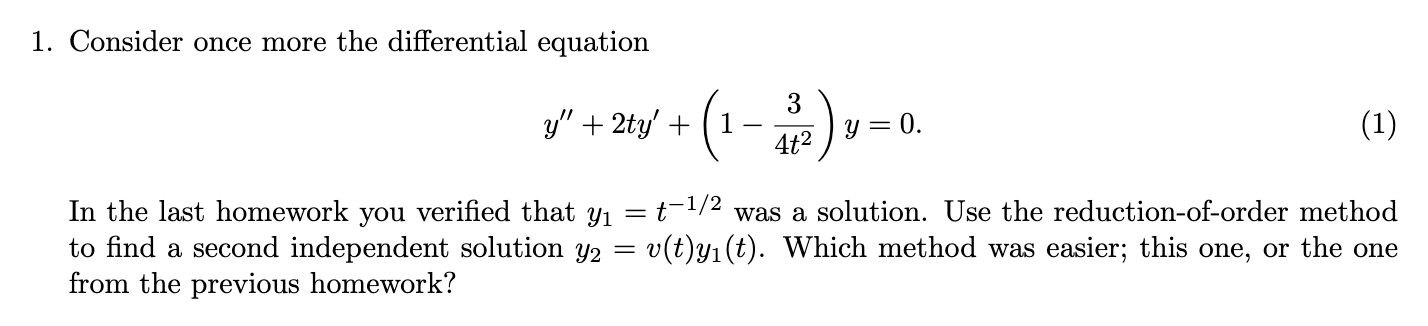
1. Consider once more the differential equation 3 \" 2t ' 1 = . 1 y + y + ( 49) y ( ) In the last homework you veried that y1 = f\"2 was a solution. Use the reductionoforder method to nd a second independent solution y2 = o(t)y1(t). Which method was easier; this one, or the one from the previous homework? Substituting y, = t' into ODE gives a polynomial in t. Setting coefficients to zero gives P= -1/2