Question: 1. Consider problem of approximationg numerically the definite integral I = Sof(x) dx by an approximation In with n subintervals of width h = (b

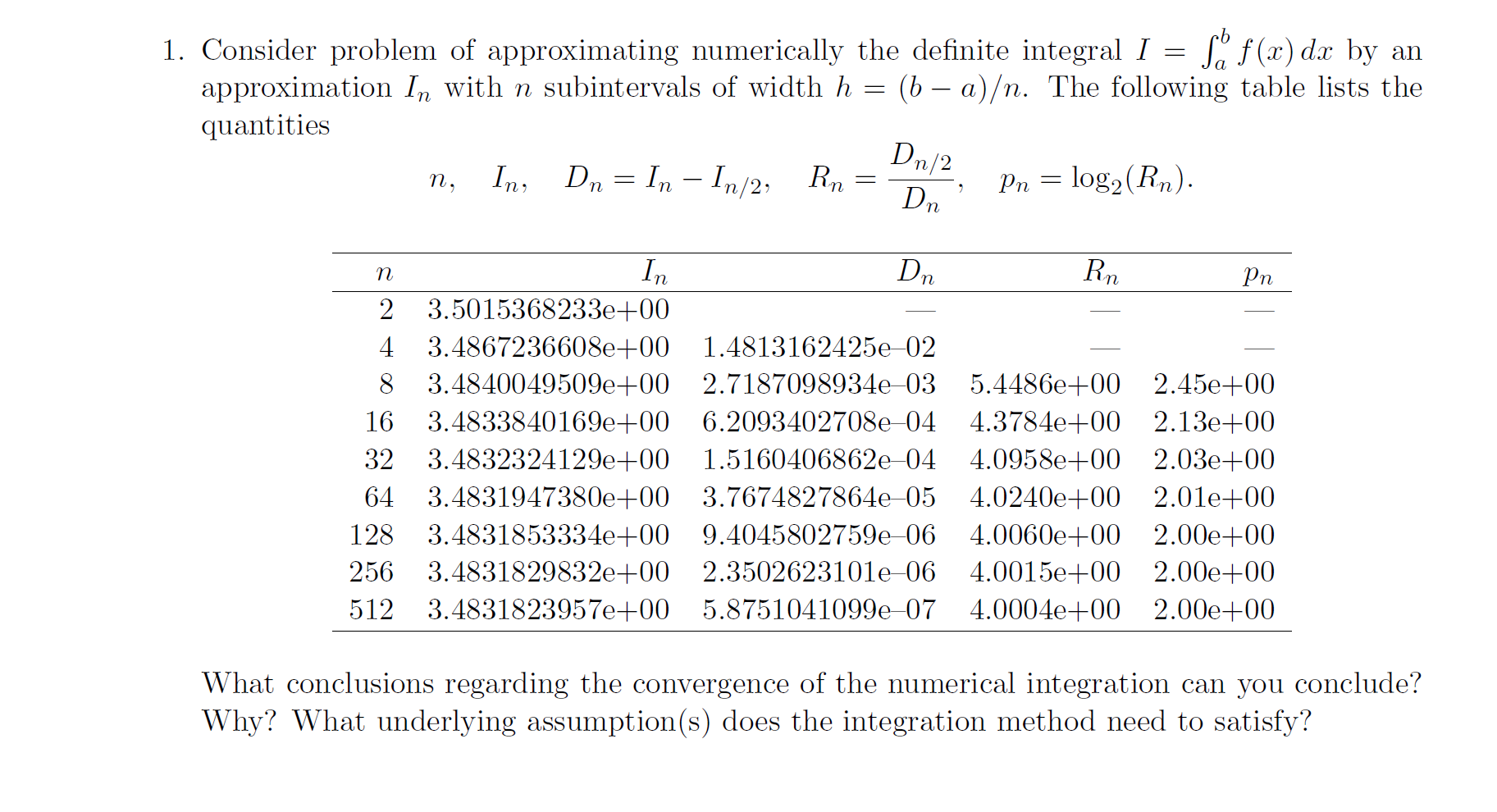
1. Consider problem of approximationg numerically the definite integral I = Sof(x) dx by an approximation In with n subintervals of width h = (b - a). The following table lists the quantities n , In, Dn = In - In/2. Rin = Dn/2 pn = 10g2(Rn). Dn n In Dn Rn Pn 2 3.5015368233e+00 4 3.4867236608e+00 1.4813162425e-02 8 3.4840049509e+00 2.7187098934e 03 5.4486e+00 2.45e+00 16 3.4833840169e+00 6.2093402708e 04 4.3784e+00 2.13e+00 32 3.4832324129e+00 1.5160406862e-04 4.0958e+00 2.03e+00 64 3.4831947380e+00 3.7674827864e-05 4.0240e+00 2.01e+00 128 3.4831853334e+00 9.4045802759e-06 4.0060e+00 2.00e+00 256 3.4831829832e+00 2.3502623101e-06 4.0015e+00 2.00e+00 512 3.4831823957e+00 5.8751041099e-07 4.0004e+00 2.00e+00 What conclusions regarding the convergence of the numerical integration can you conclude? Why? What underlying assumption(s) does the integration method need to satisfy

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Mathematics Questions!

Unit 6 Study Guide- The Definite Integral 1 . Base your answer on x 0 1 2 3 4 S(x) 0 1.2 4.3 6.5 1 For the function whose values are given in the table above. approximate / f(x)dx using a Riemann Sum...

Areas of regions under curves can be approximated by evaluating Riemann sums, which give the area of a collection of rectangles. In this project, we investigate special cases in which is it possible...

14. [OIZ Points] DETAILS PREVIOUS ANSWERS SCALC8 2.8.048. MY NOTES ASK YOUR TEACHER | PRACTICE ANOTH Two people start from the same point. One walks east at 6 mi/h and the other walks northeast at 1...

A table of values of an increasing function f is shown. time left... 10 14 18 22 26 30 2:20: 40 f(x ) -12 -9 Use the table to find lower and upper estimates for (( x ) dx . ( Use five equal...

Consider the function f(x)=x-5x+7x-3. (a) (i) Find f'(x) and "(x). [1 mark] (ii) Using Newton's method, find a root of f(x) starting with po =0.9 by completing the following table. Use FOUR decimal...

Math 104A Homework #3 Instructor: Lihui Chai General Instructions: Please write your homework papers neatly. You need to turn in both full printouts of your codes and the appropriate runs you made....

Math 1172 Project #1 Applications of Integration Due: Tuesday, September 12 Name(s): - - - - - - - - - - - - - - - - - - - - Description - - - - - - - - - - - - - - - - - - - The definite integral is...

7:05 Search webassign.net Description 1. [-/1.04 Points] DETAILS SCALCET9 5.1.002. MY NOTES ASK YOUR TEACHER PRACTICE ANOTHER The graph of the function f is given. y = f(x) 10 12 (a) Use six...

Math 104A Homework #2 Instructor: Lihui Chai General Instructions: Please write your homework papers neatly. You need to turn in both full printouts of your codes and the appropriate runs you made....

Downloaded 02/28/15 to 132.174.255.3. Redistribution subject to SIAM license or copyright; see http://www.siam.org/journals/ojsa.php 15.7. Exercises 475 changes and we laugh no more. While...

Find io in the circuit of Fig. 10.93 using superposition. 20 uF 0 cos 2000r V + 80 100 40 mH 2 sin 4000r A 60 24 V

alternative data mining models CRM and DM Assignment 1 1. Given the following data, alternative data mining models have been applied on a test set of data. What appears to be the best model? Subject...

QUESTION 1 9 3 points cost of $ 8 per pound to produce. What is the differential cost of producing Product Y ? $ 1 5 per pound $ 2 3 per pound . $ 8 per pound $ 5 per pound

milestone in project management. Which one of the sentence is an example of Milestone a) Build the foundation b) Wall painted c) Foundation d) Execute land scape work e) Infrastructure

2. In this chapter, the reader should reflect on the following concepts: Context, winwin, win-lose, ambiguity, mental model, point of reference.

2. In this chapter, the reader should reflect on the following concepts: Patterns, symmetrical relationships, complementary relationships.

1. To provide insight into how setting an overly narrow boundary can give a mes-sage a specific meaning, while setting a wider boundary can give a completely different meaning.