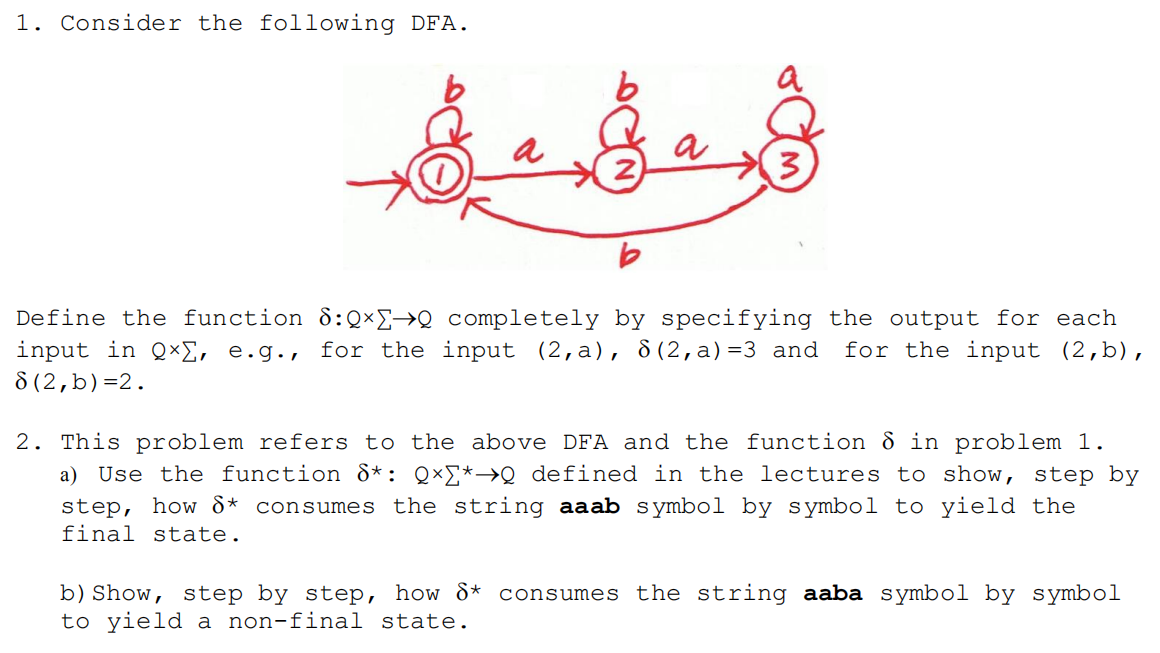
1. Consider the following DFA. b Define the function 8:0*=Q completely by specifying the output for each input in ex, e.g., for the input (2,a), 8 (2, a) =3 and for the input (2,b), 8 (2,b)=2. 2. This problem refers to the above DFA and the function d in problem 1. a) Use the function S*: Q*I*> defined in the lectures to show, step by step, how 6* consumes the string aaab symbol by symbol to yield the final state. b) Show, step by step, how 8t consumes the string aaba symbol by symbol to yield a non-final state. 3. For each of the five languages given below, show a state diagram of a DFA that recognizes the language. Use as few states as you can. E = {a, b}. For L3, L4 and L5, use the algorithms given in the lectures. Li= { x x ends with the substring bab} L2= {x | x has an even number of b's} L3=Li U L2 L4=Li n L2 L5=Li' (Note: Li' denotes the complement of Li) In 4. Consider the language L = { ba2n | n ? 1}, where aan denotes 2n a's. words, every sentence in L is the letter b followed by 2n a's for some integer n ? 1. For example, b, ba and baaa are not in L but baa, baaaa and baaaaaa are in L. Show the 5 shortest strings that are pairwise distinguishable with respect to L, and for each pair of the 5 strings (there are 10 pairs), show a distinguisher. 1. Consider the following DFA. b Define the function 8:0*=Q completely by specifying the output for each input in ex, e.g., for the input (2,a), 8 (2, a) =3 and for the input (2,b), 8 (2,b)=2. 2. This problem refers to the above DFA and the function d in problem 1. a) Use the function S*: Q*I*> defined in the lectures to show, step by step, how 6* consumes the string aaab symbol by symbol to yield the final state. b) Show, step by step, how 8t consumes the string aaba symbol by symbol to yield a non-final state. 3. For each of the five languages given below, show a state diagram of a DFA that recognizes the language. Use as few states as you can. E = {a, b}. For L3, L4 and L5, use the algorithms given in the lectures. Li= { x x ends with the substring bab} L2= {x | x has an even number of b's} L3=Li U L2 L4=Li n L2 L5=Li' (Note: Li' denotes the complement of Li) In 4. Consider the language L = { ba2n | n ? 1}, where aan denotes 2n a's. words, every sentence in L is the letter b followed by 2n a's for some integer n ? 1. For example, b, ba and baaa are not in L but baa, baaaa and baaaaaa are in L. Show the 5 shortest strings that are pairwise distinguishable with respect to L, and for each pair of the 5 strings (there are 10 pairs), show a distinguisher