1

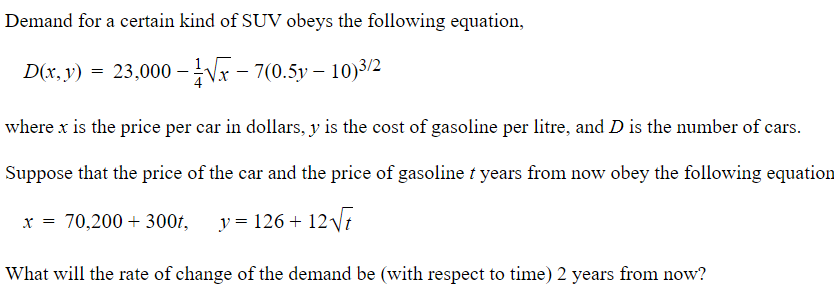
Consider the following function. g\" v) = 379+T+42x (:1) Find the critical point of g. If the critical point is (a, b) then enter 'aJJ' (without the quotes} into the answer box. ([1) Using your critical point in (a), nd the value of 130:, b) from the Second Partials test that is used to classify the critical point. (c) Use the Second Partials test to classify the critical point from {a}. Demand for a certain kind of SUV obeys the following equation, D(x,y) = 23,000 3114 7(0.5y10)3l2 where x is the price per car in dollars, y is the cost of gasoline per litre, and Dis the number of cars. Suppose that the price of the car and the price of gasoline tyears from now obey the following equation x = TD,200+3[)D:, y=126+12\\/; What will the rate of change of the demand be (with respect to time] 2 years from now