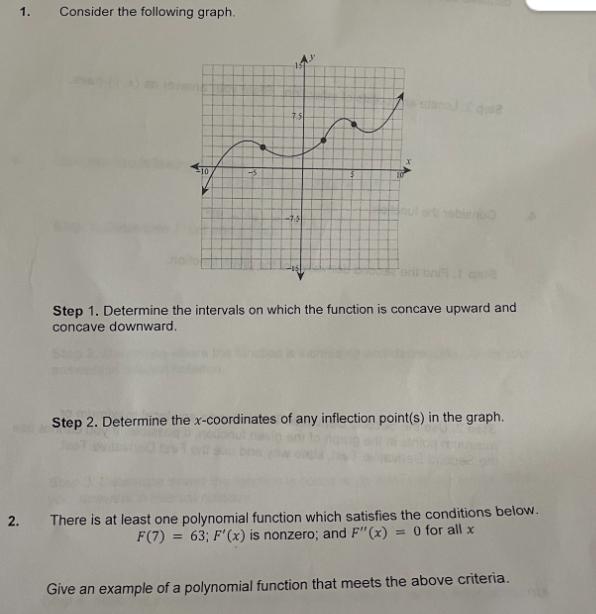
1. Consider the following graph. 10 7.5 -70 Step 1. Determine the intervals on which the function is concave upward and concave downward. Step 2. Determine the x-coordinates of any inflection point(s) in the graph. 2. There is at least one polynomial function which satisfies the conditions below. F(7) 63; F'(x) is nonzero; and F" (x) = 0 for all x = Give an example of a polynomial function that meets the above criteria. 3. Consider the function: f(x)=-5x +120x + 3x - 1 Step 1. Determine the intervals on which the function is concave upwards or concave downwards. Step 2. Locate any points of inflection. State your answer as (x, y)-pairs. 4. Consider the function: f(x) = (x - 9) Step 1. Find the second derivative of the given function. Step 2. Use the Second Derivative Test to locate any local maximum or minimum points in the graph of the given function, if possible. If you cannot use the Second Derivative Test, state why and use the First Derivative Test.