1. consider the following LP problem and its optimal tableau shown below.

Maximize z = 3x₁ + 2x₂ + 5x₃

s.t. x₁ + 2x₂ + x₃ 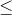5 3x1 + 2x3 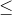6

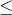x1 + 4x2 2

1) Write the dual problem.

optimal Tableau:

	x1	x2	x3	s1	s2	s3	RHS
z	5	0	0	0	2.5	0.5	16
s1	-1	0	0	1	-0.5	-0.5	1
x3	1.5	0	1	0	0.5	0	3
x2	0.25	1	0	0	0	0.25	0.5

2) How large can c₁ (the coefficient of x₁ ) in the objective function be made with keeping the current optimal solution.

3) How large can b₁ (the first constraint resource) be made without violate feasibility?

4) Suppose that the following constraint is added to the problem: 2x₁ + x₂ + x₃ 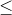4. Find the optimal solution and value.

Transcribed image text