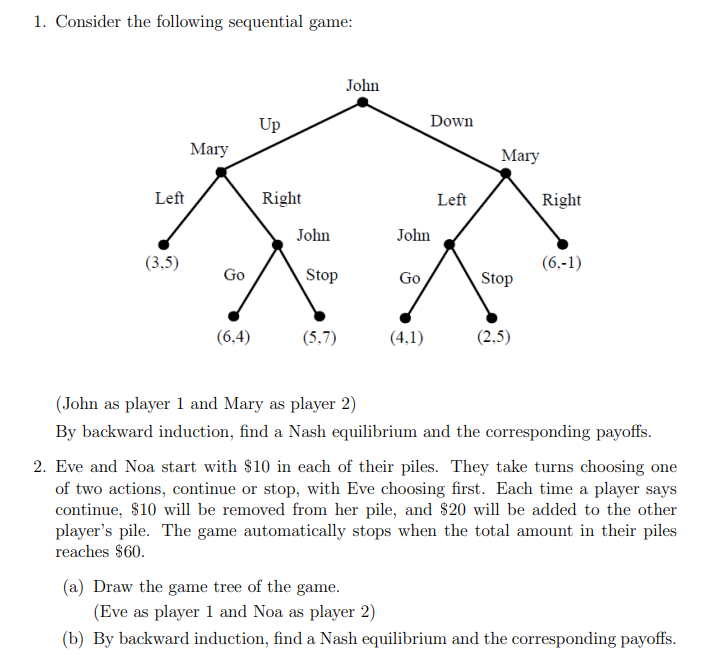
1. Consider the following sequential game: (John as player 1 and Mary as player 2) By backward induction, find a Nash equilibrium and the corresponding payoffs. 2. Eve and Noa start with $10 in each of their piles. They take turns choosing one of two actions, continue or stop, with Eve choosing first. Each time a player says continue, $10 will be removed from her pile, and $20 will be added to the other player's pile. The game automatically stops when the total amount in their piles reaches $60. (a) Draw the game tree of the game. (Eve as player 1 and Noa as player 2) (b) By backward induction, find a Nash equilibrium and the corresponding payoffs. 1. Consider the following sequential game: (John as player 1 and Mary as player 2) By backward induction, find a Nash equilibrium and the corresponding payoffs. 2. Eve and Noa start with $10 in each of their piles. They take turns choosing one of two actions, continue or stop, with Eve choosing first. Each time a player says continue, $10 will be removed from her pile, and $20 will be added to the other player's pile. The game automatically stops when the total amount in their piles reaches $60. (a) Draw the game tree of the game. (Eve as player 1 and Noa as player 2) (b) By backward induction, find a Nash equilibrium and the corresponding payoffs