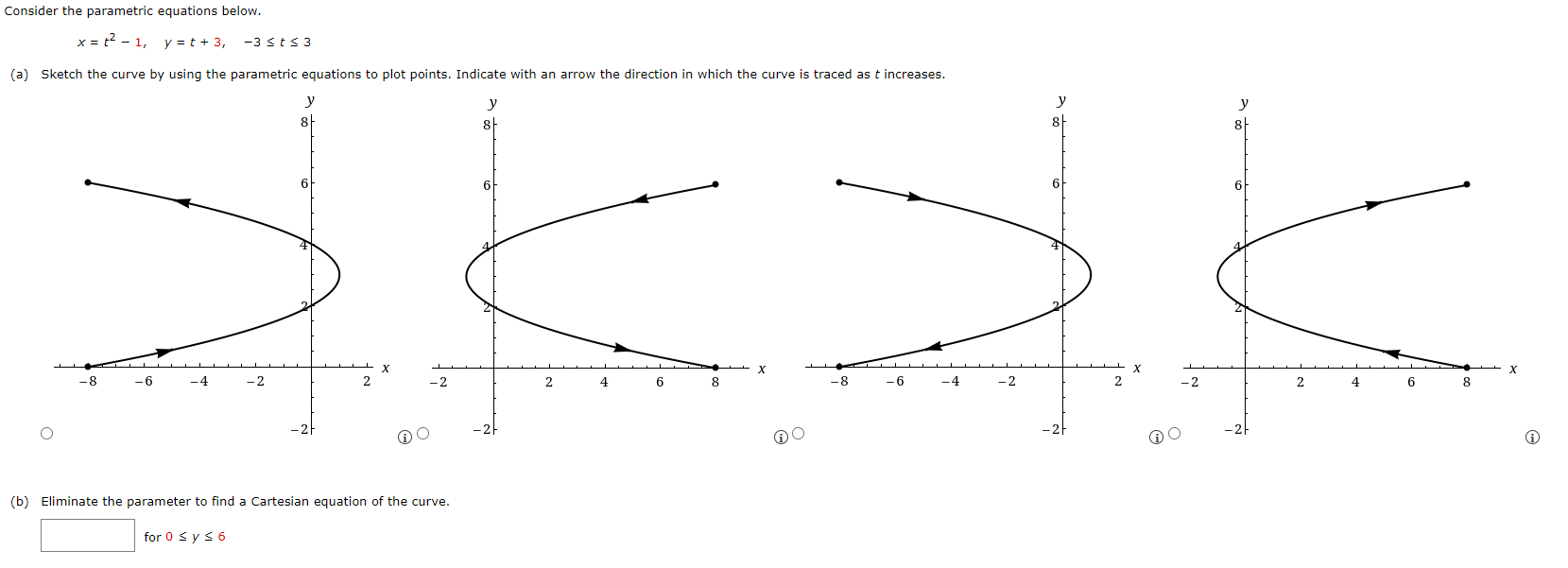
Question: 1. Consider the parametric equations below. x = tz - 1, y=t+3, -3Ets3 (a) Sketch the curve by using the parametric equations to plot points.

1.
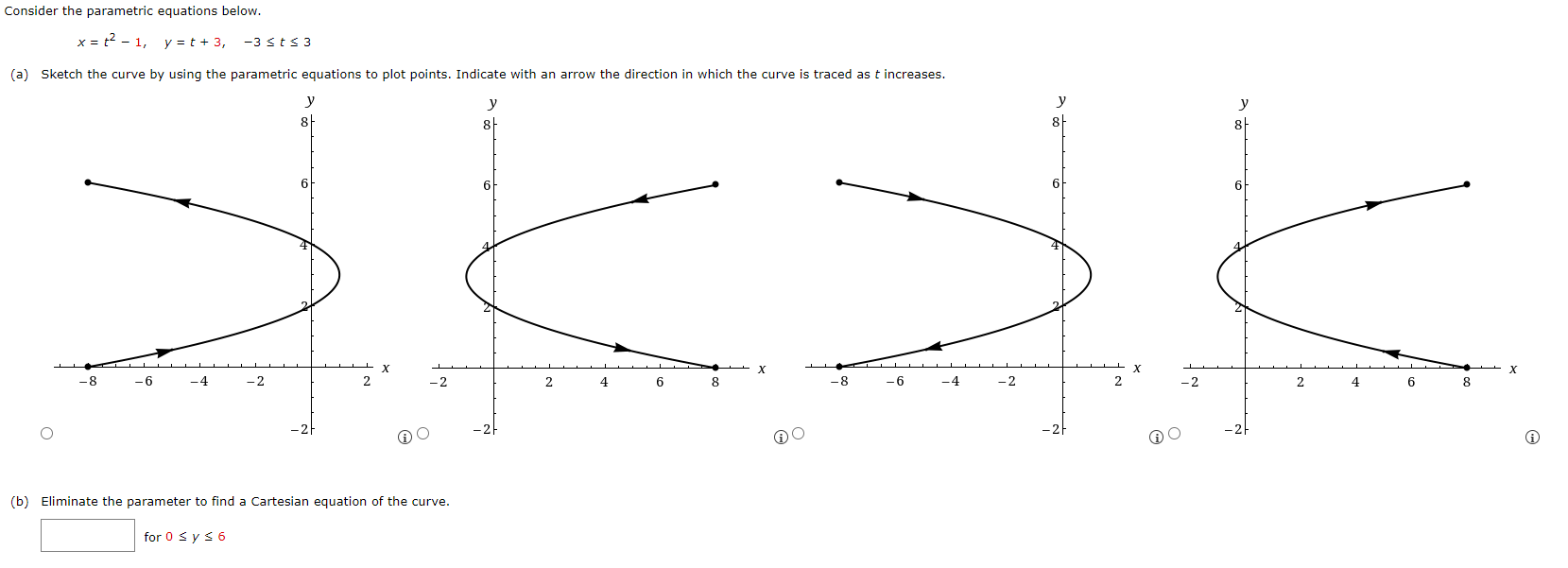

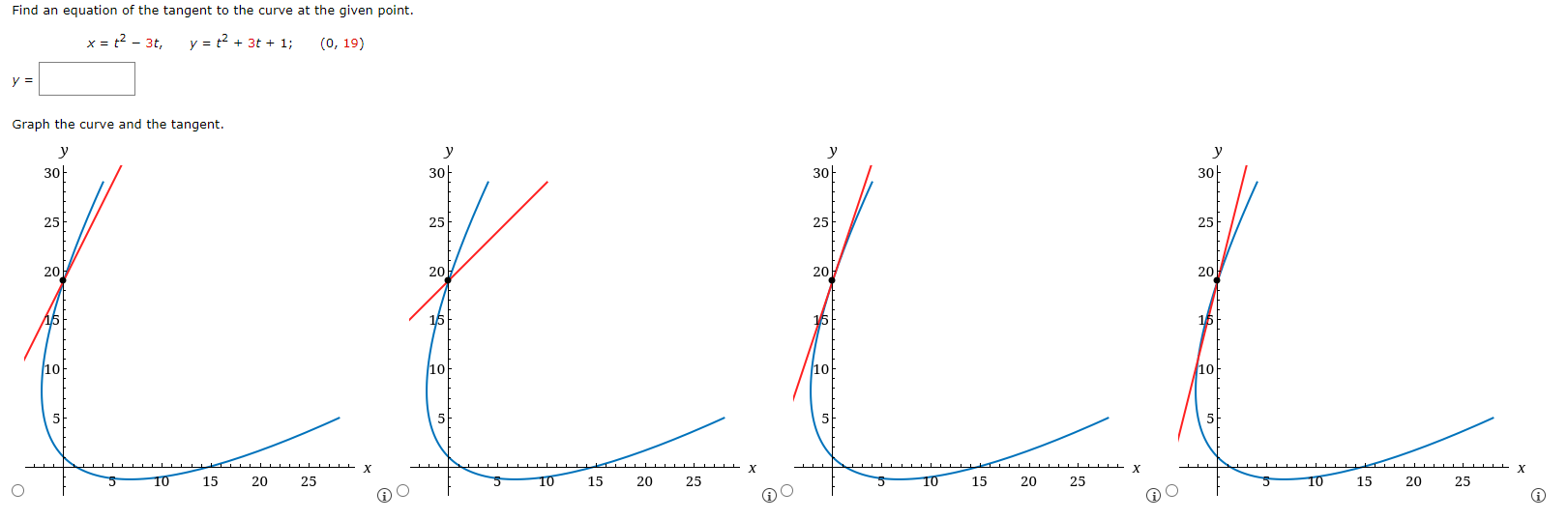
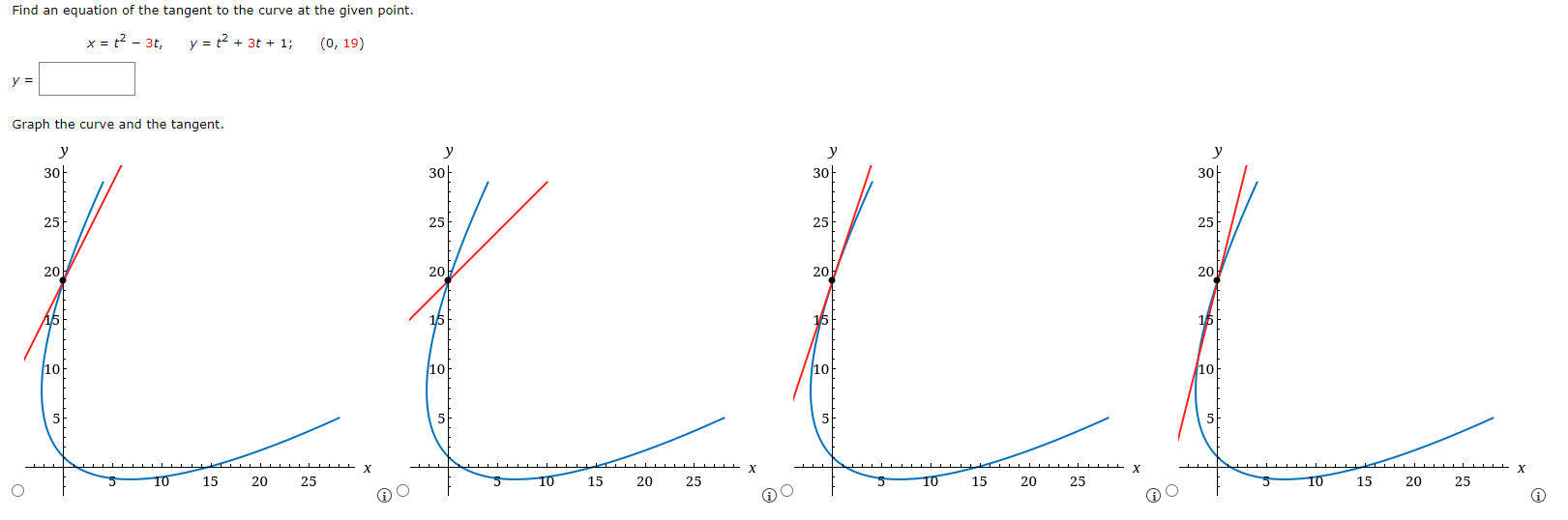
Consider the parametric equations below. x = tz - 1, y=t+3, -3Ets3 (a) Sketch the curve by using the parametric equations to plot points. Indicate with an arrow the direction in which the curve is traced as t increases. y 6 6 X X X X -8 -6 -4 -2 2 -2 2 4 6 8 -8 -6 -4 -2 2 -2 2 4 6 8 O -21 AO -21 -2 -21 (b) Eliminate the parameter to find a Cartesian equation of the curve. for O E y s 6Find an equation of the tangent to the curve at the point corresponding to the given value of the parameter. x=t'+1, y=tl0+ t; t= -1 V=Find an equation of the tangent to the curve at the given point. x = tz - 3t, y = tz + 3t + 1; (0, 19) y = Graph the curve and the tangent. 30 30/ 30/ 25- 30 25- 25 201 25 204 20 15 20 15- 10 16 10- 5 10- 5 5/ 3 5 10 15 X 20 25 10 15 X 20 25 10 15 X 20 25 10 15 X 20 25 A
Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


