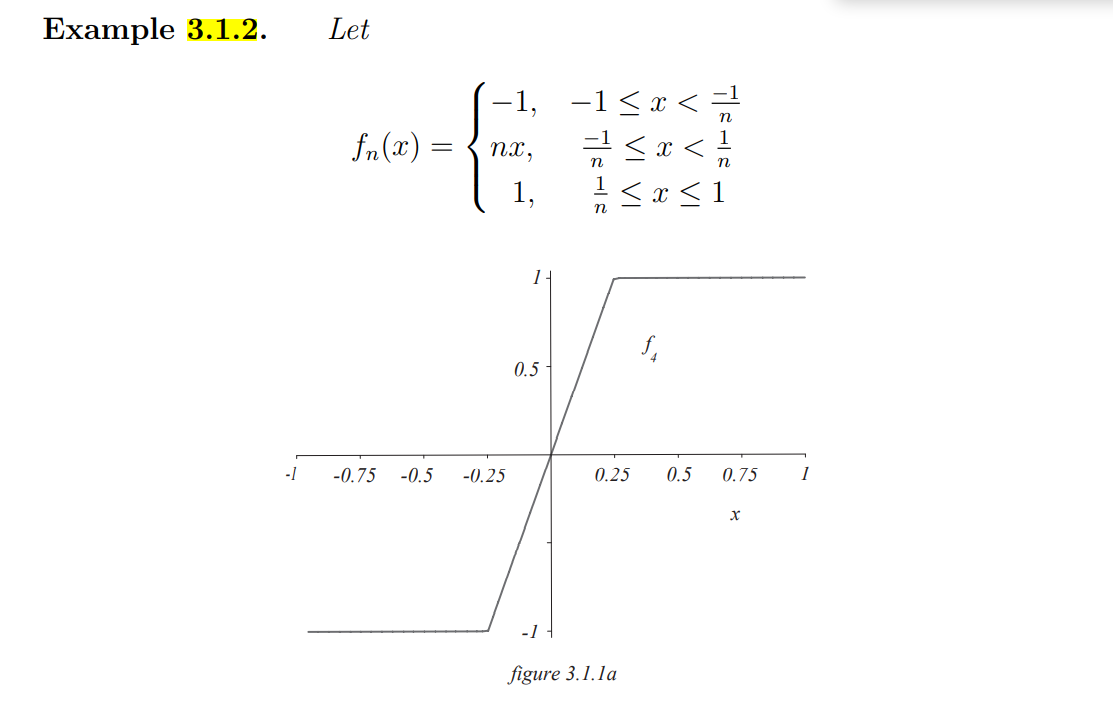
1. Consider the sequence of functions fn : R - R defined in Example 3.1.2, which converges pointwise to f : R - R. a) Use one of the results of $3.2.2 to deduce that the convergence of fn to f cannot be uniform. b) Show directly from the definition that the convergence of fn to f is not uniform.Example 3.1.2. Let 1, -1 0 there exists N E Z+ such that for all m, n 2 N and all x E I we have Ifm(x) - fn(2) | Lm and fn(x) > In give us bounds on the first and last terms: there exists o > 0 such that if 0