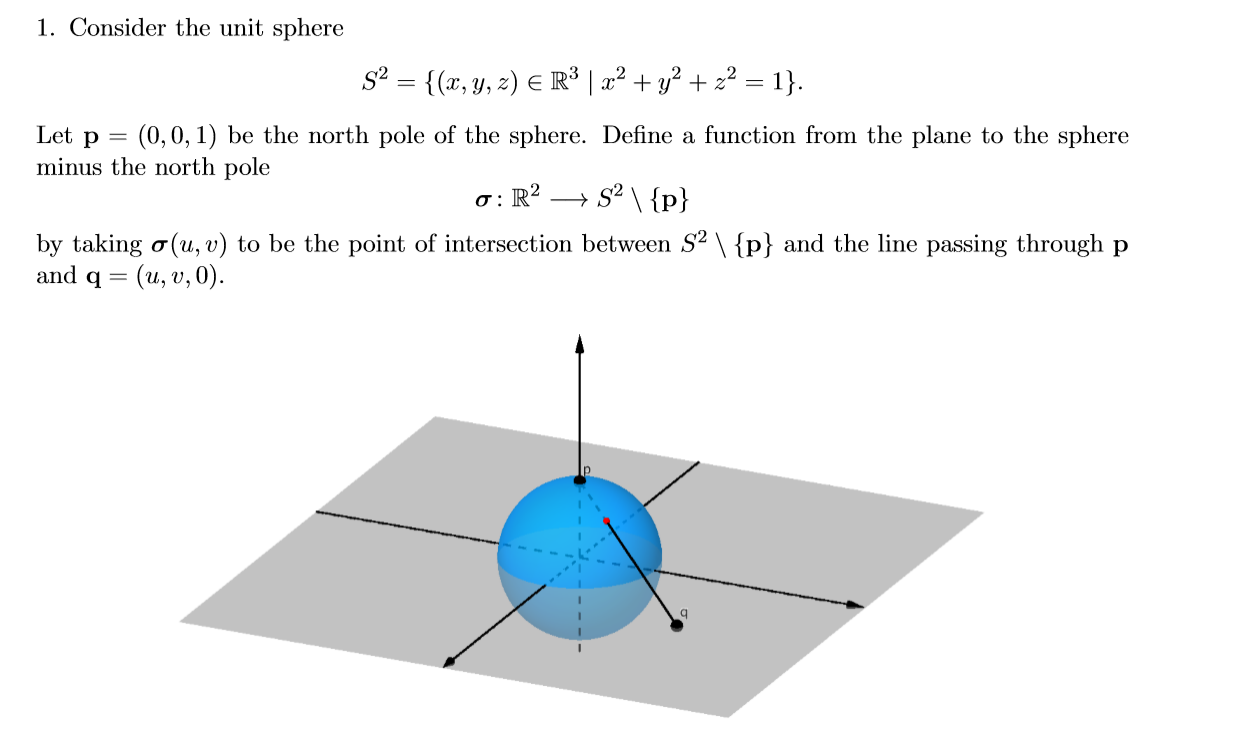
1. Consider the unit sphere 32 = {(w,y,z) E R3 |w2 +y2 +22 = 1}. Let p = (0, 0, 1) be the north pole of the sphere. Dene a function from the plane to the sphere minus the north pole 01R2>S2\\{p} by taking 0(u, v) to be the point of intersection between S2 \\ {p} and the line passing through p and q = (u,v,0). (a) Give an explicit formula for a(u, v) as a function of u, v. [Hintt parametrize the line through p and q by (1 t)p + tq, then intersect with the sphere and solve for t.] (b) If (x, y, z) is a point in $2\\{p}, give an explicit formula for 6103, 3;, 2) as a function of 3:, y, z. (c) Show that 0' is a regular surface patch on .92. \"n .1 n .- n01 .1. \"(H km. 1 .1 I. \"I