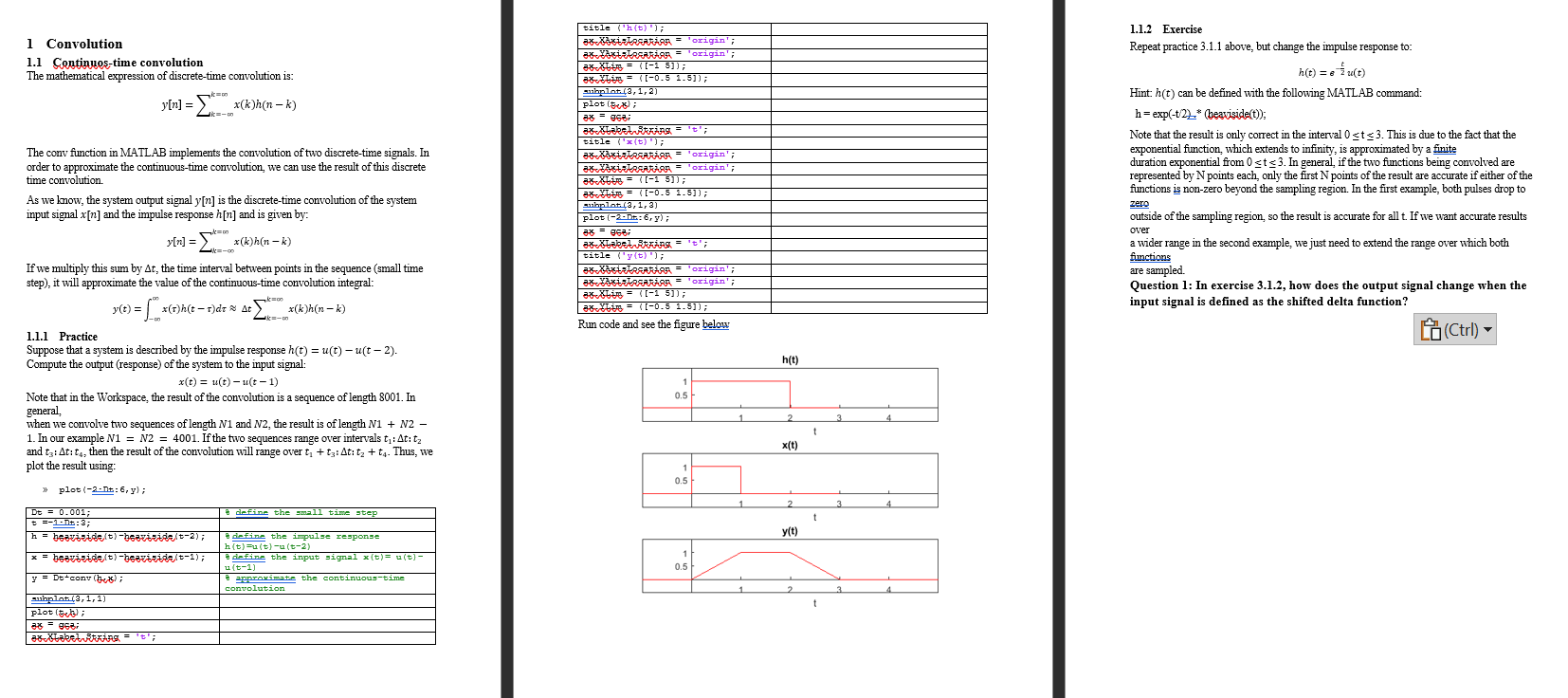
1 Convolution Repeat practice 3.1.1 above, but change the impulse response to: 1.1 Continues-time convolution The mathematical expression of discrete-time convolution is: h(t)=e2tu(t) y[n]=k=k=x(k)h(nk) Hint: h(t) can be defined with the following MATLAB command: h=exp(t/2)( heaxisides (t)); Note that the result is only correct in the interval 0t3. This is due to the fact that the The conv function in MATLAB implements the convolution of two discrete-time signals. In exponential function, which extends to infinity, is approximated by a finit order to approximate the continuous-time convolution, we can use the result of this discrete time convolution. duration exponential from 0t3. In general, if the two functions being convolved are represented by N points each, only the first N points of the result are accurate if either of the As we know, the system output signal y[n] is the discrete-time convolution of the system functions is non-zero beyond the sampling region. In the first example, both pulses drop to zero input signal x[n] and the impulse response h[n] and is given by: zero ovitside of the sampling region, so the result is accurate for all t. If we want accurate results a wider range in the second example, we just need to extend the range over which both If we multiply this sum by t, the time interval between points in the sequence (small time functions step), it will approximate the value of the continuous-time convolution integral: Question 1: In exercise 3.1.2, how does the output signal change when the y(t)=x()h(t)dtk=k=x(k)h(nk) input signal is defined as the shifted delta function? 1.1.1 Practice Suppose that a system is described by the impulse response h(t)=u(t)u(t2). Compute the output (response) of the system to the input signal: x(t)=u(t)u(t1) Note that in the Workspace, the result of the convolution is a sequence of length 8001. In general, when we convolve two sequences of length N1 and N2, the result is of length N1+N2 1. In our example N1=N2=4001. If the two sequences range over intervals t1:t:t2 and t3:t:t4, then the result of the convolution will range over t1+t3:t:t2+t4. Thus, we plot the result using