Question: 1. Derive equation (6.9) k=1, 2, ..., n. note that: . 2. Derive the CAPM formula for by using equation (6.9 above). Apply (6.9) to
1. Derive equation (6.9) 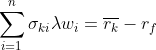 k=1, 2, ..., n.
k=1, 2, ..., n.
note that: 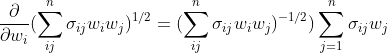 .
.
2. Derive the CAPM formula for 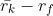 by using equation (6.9 above). Apply (6.9) to asset k and to the market itself. Note that:
by using equation (6.9 above). Apply (6.9) to asset k and to the market itself. Note that: 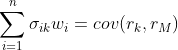 .
.
1. Derive equation (6.9) sum{i=1}^{n}sigma {ik}w{i} = cov(r{k}, r{M}) .bar{r{k}}-r{f} by using equation (6.9 above). Apply (6.9) to asset k and to the market itself. Note that: frac{partial}{partial w{i}}(sum{ij}^{n}sigma {ij}w{i}w{j})^{1/2}=(sum{ij}^{n}sigma {ij}w{i}w{j})^{-1/2})sum{j=1}^{n}sigma {ij}w{j} .2. Derive the CAPM formula for sum{i=1}^{n}sigma{ki} lambda w{i}=overline{r{k}} -r{f} k=1, 2, ..., n.note that: 1. Derive equation (6.9) sum{i=1}^{n}sigma {ik}w{i} = cov(r{k}, r{M}) .bar{r{k}}-r{f} by using equation (6.9 above). Apply (6.9) to asset k and to the market itself. Note that: frac{partial}{partial w{i}}(sum{ij}^{n}sigma {ij}w{i}w{j})^{1/2}=(sum{ij}^{n}sigma {ij}w{i}w{j})^{-1/2})sum{j=1}^{n}sigma {ij}w{j} .2. Derive the CAPM formula for sum{i=1}^{n}sigma{ki} lambda w{i}=overline{r{k}} -r{f} k=1, 2, ..., n.note that
Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


