1. Describe a small example for why this algorithm is a good candidate for dynamic programming. Hint: pick a number with multiple factors. You may use Wolfram Alpha (or some other calculator) to compute gcd's.

2. What data structure would you use in order to store the solutions to subproblems?

3. What is a reasonable sentinel value to indicate that the algorithm has not yet computed 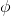(n)?

Euler's Totient function (or Euler's Phi function. is a function that accepts a positive integer n and returns how many positive integers less than n are relatively prime to n. (That is, they have greatest common divisor of 1 with n As an example, consider computing (12). We can see from the following table that only 1, 5, 7, and 11 are relatively prime to 12, so o(12) 4. z gcd(z, 12) 10 11 The naive EulerPhi algorithm below computes Euler's Phi recursively based on the following recurrence: if n is prime or 1 o(n) (a) (b) ged bi, where of and b n/a (god (a,b)) a is a factor n