Question: 1. Design a Turing machine which recognizes the language consisting of all strings of Os whose length is a power of 2. i.e., it

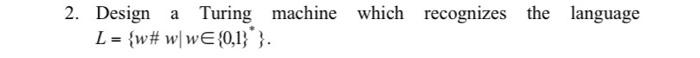
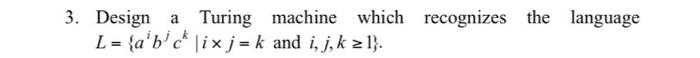









![N N such that f(a, b) = [a/b] (c) f:N N such](https://dsd5zvtm8ll6.cloudfront.net/si.experts.images/questions/2022/08/62fb1ba2cc966_1660623776958.jpg)
![that f(n) = [log, n]. 7. Define Nondeterministic Turing machines to accept](https://dsd5zvtm8ll6.cloudfront.net/si.experts.images/questions/2022/08/62fb1badf31ce_1660623784659.jpg)
1. Design a Turing machine which recognizes the language consisting of all strings of Os whose length is a power of 2. i.e., it decides the language L = {0" | n 0}. Turing machine which recognizes the language 2. Design a Turing L = {w#w|wE {0,1}*}. 3. Design a Turing machine L = {a'b'ck |ix j = k and i, j, k 1}. which recognizes the language 4. Design a deterministic Turing machine (DTM) to accept the language L = {a'b'c' |iz0}. 5. Define a DTMs to accept the following languages. Specify the 5-tuple in each. (Use multi-tape machine if necessary). (a) {xxx {0,1}} (b) {xx(0,1) and x = x^} 6. Design DTMs to compute the following functions. (Input number can be in unary, i.e., n is encoded as 1"). (a) Successor function: f:N N where f(n) = n +1. (b) f: Nx N N such that f(a, b) = [a/b] (c) f:N N such that f(n) = [log, n]. 7. Define Nondeterministic Turing machines to accept the following languages. (a) {xx x= {0,1}} (b) (xx(0,1) and x = x} 8. Define a multiheaded Turing machine, a model in which each tape can have k tape heads. Prove that a Deterministic Turing Machine (DTM) with one work tape can simulate a two-headed Turing machine. 9. Design a Turing machine which computes the function f(n,n) = min(n, n) for all non-negative integers n, and n. 10. Design a Turing machine which computes the function f(n) = 3 if n 5 and f(n) = 0 if n =0, 1, 2, 3 or 4. 11. Construct a Turing machine which computes the function f(n) = n mod 5. 12. Design a Turing machine which recognizes the set (0"1"2" In 0). 13. Design a TM that recognizes the set of all bit strings that contain an even number of 15. 14. Construct a TM that recognizes the set of all bit strings which end with a 0. 15. Design a Turing machine with tape symbols 0, 1 and B that given a bit string as input, replaces all but the leftmost 1 on the tape with Os and does not change any of the other symbols on the tape. 16. Design a TM with tape symbols 0, 1 and B that replaces the first 0 with a 1 and does not change any of the other symbols on the tape. 17. Design a TM that recognizes the set (02"1" |nz0}. 18. Show that the recursiveness problem of Type-0 grammars is unsolvable. 19. Show that the problem of determining whether or not a TM over {0,1} will print ever the symbol 1, with a given tape configuration is unsolvable. 20. Show that there exists a TM for which the halting problem is unsolvable.
Step by Step Solution
3.46 Rating (172 Votes )
There are 3 Steps involved in it
1 Design for a Turing machine that recognizes the language L 0 n 0 The tape alphabet is 0 1 where 0 represents a blank symbol and 1 represents the input symbol The initial state is q0 and the only acc... View full answer

Get step-by-step solutions from verified subject matter experts


