Question: 1. Determine the adjoint operator L* and corresponding adjoint boundary condi- tions for the following boundary value problem: Lu = u(x) - (sin x) u'

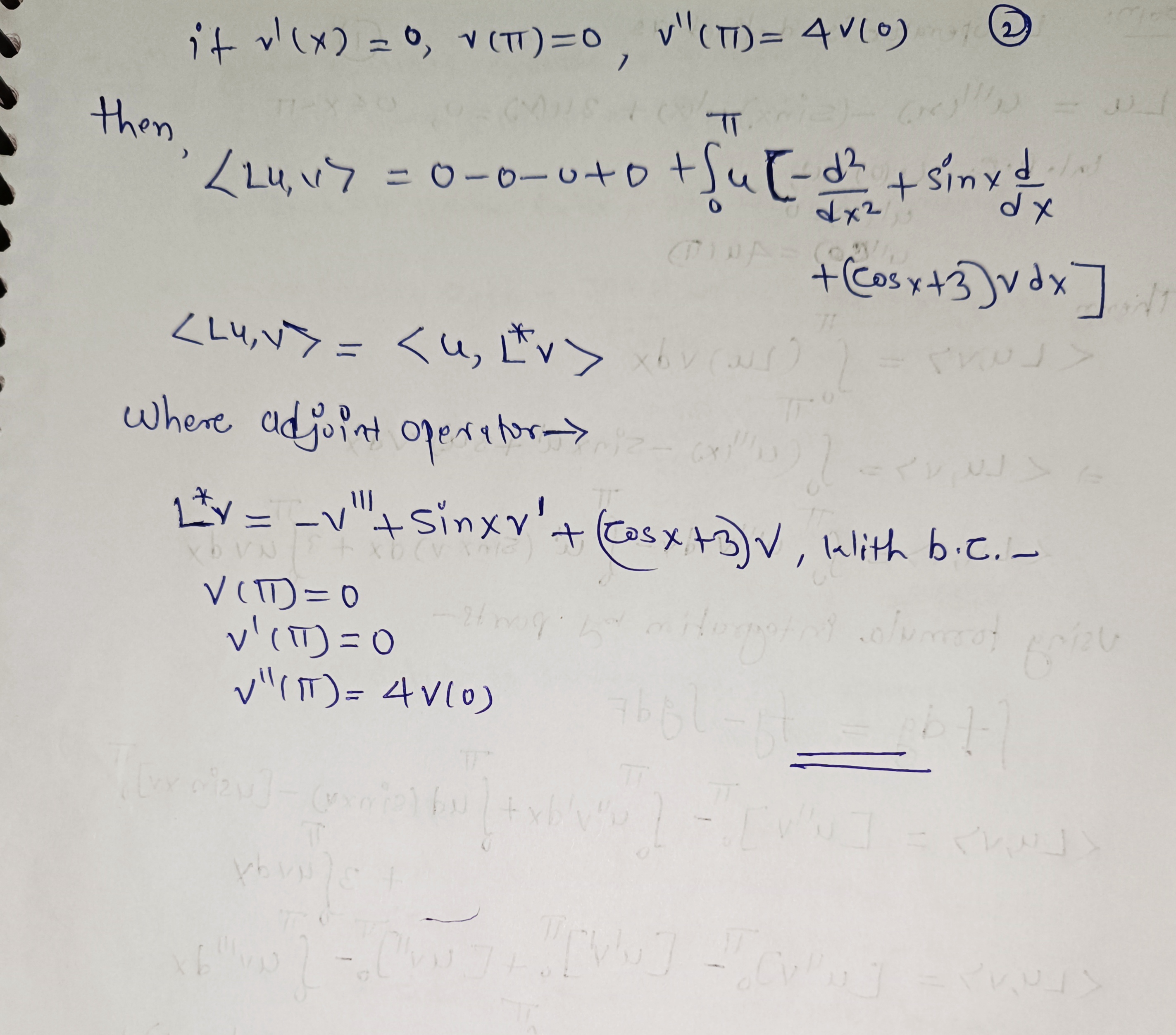
1. Determine the adjoint operator L* and corresponding adjoint boundary condi- tions for the following boundary value problem: Lu = u"(x) - (sin x) u' (x) + 3u(x) = 0, 05x51 u(0) = 0 u'(0) = 0 u"(0) = 4u( T) The symbol ' represents derivative with respect to the independent variable x.som : 1 operator is defined as ( ) (1) x) for Lu = ullens - (sinx)ulus+ 3 4(x)=0, 0EXSIT lal . B. e. 4 0 ) = 0, 1/ 40-0-0 ul ( 0 ) = 0 41 20 ) = 441D Thenn IT = (u"(*) - sinxu + sw. vax ibb smells = [ ullv dx- / u( sinx v> dx + 3fundx Using toomula integration by ports- O = ( 17 ) V Stag = fg- SadF (OJVA = ( 71 )/ V IT = [u"v]. - [ u"v'dx+ ud( sinxv) -[usin x]." + 3 / uvdy Juvax + Ju ( cosx y + sinx v ' + 3 v ) d x O There fore u satisfies boundry faluc Conditions- U ( 0 ) = 0, U 10) = 0, ull10) = QUITD 20 , = U' ( TDV( TT ) - U" LOSVIOS - UITDV ITTY - ULOV ' 10) + UCTT)~" (TD) - uCODY (of + Su[- v"+ (cosx+ 3 )y +sinxv ' ] dx V 10 ) - U/ TT ) V / ( IT ) + O( TT ) V " ITT Su [- ul + sinxN't (cosx+ 3) vax]it v ( x ) = 0 , V ( TT ) = 0 , V " ( TD ) = 4v (0 ) then LLY,NY = 0-0-uto+Jur-d2 dxz + sinxd. dx + ( cos* +3) vax ] LLY,V>=

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Mathematics Questions!

Thank u guys:) This is the reference pages but the questions are the last 3 pictures . . . . Craft - Mason Wage rate VET $29.00 Hours worked 50 hours per week for 20 weeks and 40 hours per week for...

^^^^^ solve please Postopening Scenario: Your angel investors are silent in relation to the business; however, they require board meetings. for status updates on the company's nancial health....

Need Help with Computational Physics HW for python on calculating electrostatic potential. Book from Computational physics by mark newman Need it solved in Overrelaxation method: Exercise 9.3: V 0...

solve the following please PRINTER VERSION BACK End of Chapter Exercise 5.9 The following information is available for BJ Electronics Led for 2015, 2016 and 2017. 2015 2016 2017 $'000 000 $'000 000...

Tactics Mentioned? Sample Size (n): ? Number of Groups: ? Number of Treatments: ? Standard Deviation ():? Standard Error:? Mean (): ? F Statistic: ? Degrees of Freedom (df):? P-Value:? An ANOVA...

QUIZ... Let D be a poset and let f : D D be a monotone function. (i) Give the definition of the least pre-fixed point, fix (f), of f. Show that fix (f) is a fixed point of f. [5 marks] (ii) Show that...

11 (10 points) Determine the adjoint operator , for the 2nd order differential operator l, = d d X + x 2 dx dx subject to Neumann boundary conditions

(a) Determine the adjoint operator, A*(Y]. (b) Derive the normal equations (i.e., the algebraic condition that a least squares solution, X , must satisfy) and the algebraic condition for a solution,...

Problem One (25 points): Below table shows the sale history for the past 10 weeks of a furniture company. The operation manager knows that her company tolerate just one stockout per year. She was...

Jones owned a large tract of vacant land. He gave permission to a construction company building homes on land adjacent to his to drive trucks along a path across his land. Five years later, Jones...

Schedule M - 1 of Form 1 1 2 0 is used to reconcile finnscial net incoese with taxable income reported on the corporation's ilicome tax return an fotlows bet incoeseper hocls s - Alitions =...

On 1 March 2007 DB Limited issued R560 000 15% debentures at R98. The debentures were to be redeemed at par in four equal annual payments starting 28 February 2010. Required: Journalise the above...