(1) Determine whether the statement is true or false. If the statement is false, rewrite it as a true statement.

a.A 95% confidence interval for a population proportion with lower bound 0.45 and upper bound 0.51 means there is a 95% probability the population proportion is between 0.45 and 0.51.

b. The higher the degree of confidence, the larger the sample required to give a certain precision.

c. To determine the value of standard error of the mean, the total error is divided by the sample size.

d. If the size of a sample equals the size of the population, we would expect any error in estimating the population parameter.

e. We can expect some difference between sample statistics and the corresponding population parameters. This difference is called the sampling error.

(2) A researcher wishes to see if there a difference in the cholesterol levels of two groups of men. A random sample of 30 men between the ages of 25 and 40 is selected and tested. The average level is 223 with the standard deviation is 6. A second sample of 42 men between the ages of 41 and 56 is selected and tested. The average of this group is 229 with the standard deviation is 8. Assume that both variables are approximately normally distributed.

a. What is the point estimate of the mean differences of the cholesterol levels?

b. Find the 95% confidence interval for the difference of the two means.

Based on answer in (a), is there a difference in the cholesterol levels between the two groups at 5% significance level? Justify your answer.

(3) A mechanical engineer in a car manufacturing company is investigating two types of bumper guards. Random sample of 6 guards from each type were mounted on a compact car. Each car was then run into a concrete wall at 8km per hour. The following are the costs of repairs (in RM):

Bumper guard 1

305420363485300360

Bumper guard 2

405345336450400360

Assume that the costs of repairs for two types of bumper guards are approximately normally distributed.

a. What is the point estimate of the mean and standard deviation of cost of repair for bumper guard 1?

b. What is the point estimate of the mean differences of cost of repairs?

c. Assuming that the variances of cost of repairs are unequal, construct a 99% confidence interval on the mean differences of cost of repairs.

Based on the confidence interval obtained in (c), can you conclude that there is difference between average costs of repairs for two types of bumper guards? Give your reason.

(4) The manufacturer of the ColourSmart television claims that 85% of its sets last at least five years without needing a single repair. In order to test this claim, a consumer group randomly selected 400 consumers who have owned a ColourSmart television set for five years. Of these 400 consumers, 65 say that their ColourSmart television sets did need at least one repair.

a. Obtain the point estimate for the proportion of all ColourSmart television sets that have lasted at least five years without needing a single repair.

b. Determine whether the condition is satisfied to use the large sample formula. (refer to picture attached)

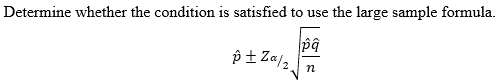
\f\f