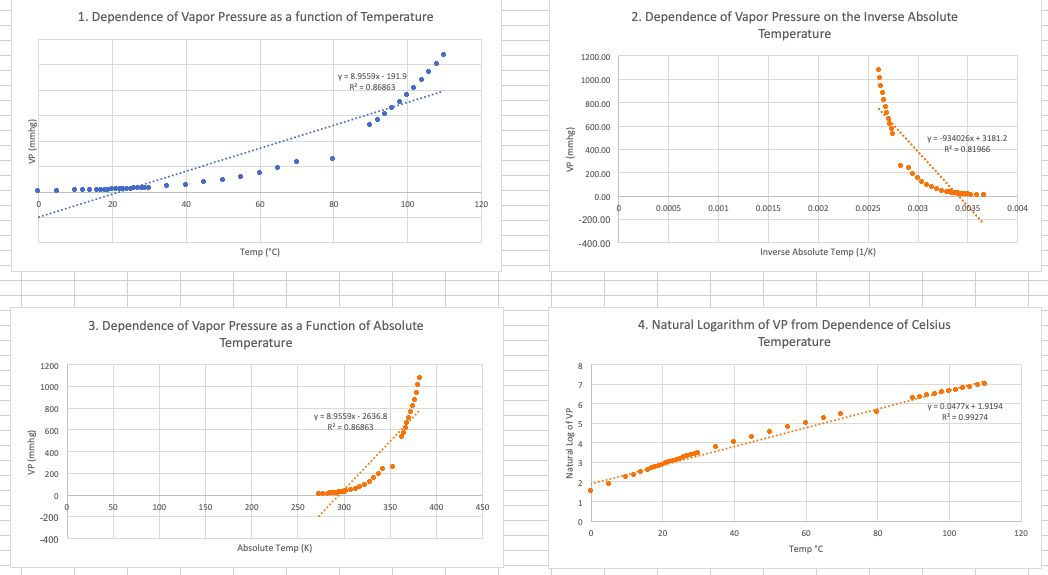
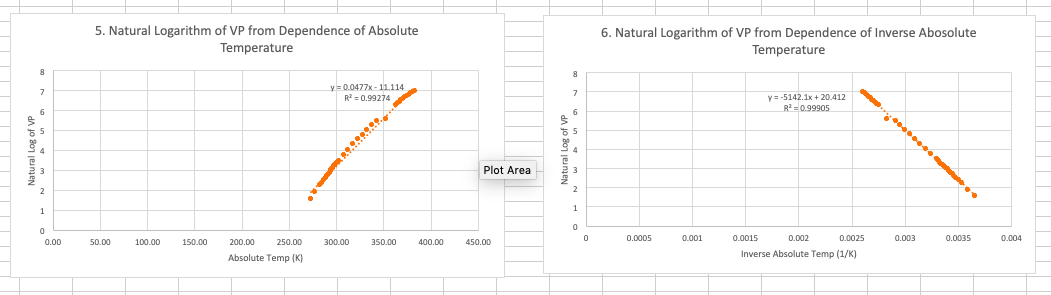
1. Determine which VPDATA graph represents the most linear trend by comparing R-squared values for the six slope-intercept equations. Ideally, if all the data points fit on the trendline, the R-squared value would be very close to 1 (0.9999). The closer an R-squared value comes to this ideal value, the more linear the data trend. Circle the chart/equation that best represents the linear data.

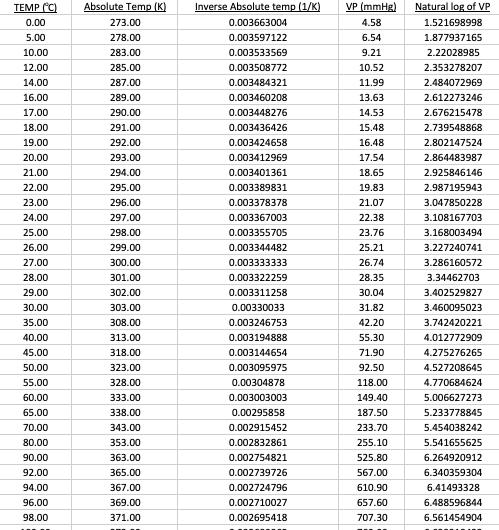
2. Locate the errant data point on the linear graph. Assume the error lies in the measurement of the dependent variable, pressure. Using its temperature value and the slope-intercept equation, calculate the corrected pressure value in units of mmHg.

3. I am also having problem with the titles. my textbook says : Every graph should have a clear statement of what it represents. Titling a graph y-axis vs. x- axis is not indicative of what the graph represents. For example, a graph displays x, y data where the x-axis data are volume values and the y-axis data are mass values. Titling the graph mass vs. volume tell us nothing more than did the axis labels. However, titling the graph Density tells us what the purpose of the graph was.

I know my titles are wrong but i dont know how to label them so they can represent simply what the graph is about. I have numbered each graph to make it easier.

1. Dependence of Vapor Pressure as a function of Temperature 2. Dependence of Vapor Pressure on the Inverse Absolute Temperature 1200.00 y = 8.9559x - 191.9 R?=0.86863 1000.00 . 800.00 600.00 Pimming VP (mmhg) 400.00 y = -934026x +3181.2 R? -0.61966 . 200.00 . 0.00 0 20 an 60 80 100 120 0.0005 0.001 0.0015 0.002 0.0025 0.003 0.003s 0.004 - 200.00 - 400.00 Temp (C) Inverse Absolute Temp (1/K) 3. Dependence of Vapor Pressure as a Function of Absolute Temperature 4. Natural Logarithm of VP from Dependence of Celsius Temperature 1200 8 1000 7 800 6 y = 8.9559x - 2636.8 R? = 0.86863 y = 0.0477x+1.9194 R = 0.99274 600 VP (mmhg) 400 200 2 0 0 50 100 150 200 250 300 1 350 400 450 -200 0 0 20 40 80 100 120 -400 60 Temp C Absolute Temp (K) 5. Natural Logarithm of VP from Dependence of Absolute Temperature 6. Natural Logarithm of VP from Dependence of Inverse Abosolute Temperature 8 8 7 y = 0.0477x - 11.114 -0.99274 7 y=-5142.1x +20.412 R?=0.99905 6 ..... 55 du jo domen 6 55 3 Plot Area 2 2 1 1 0 0.00 0.0005 0.0035 50.00 0.004 100.00 300.00 0.003 150.00 350.00 450.00 0.001 400.00 200.00 250.00 Absolute Temp (K) 0.0015 0.002 0.0025 Inverse Absolute Temp (1/K) TEMP (C) 0.00 5.00 10.00 12.00 14.00 16.00 17.00 18.00 19.00 20.00 21.00 22.00 23.00 24.00 25.00 26.00 27.00 28.00 29.00 30.00 35.00 40.00 45.00 Absolute Temp (K) 273.00 278.00 283.00 285.00 287.00 289.00 290.00 291.00 292.00 293.00 294.00 295.00 296.00 297.00 298.00 299.00 300.00 301.00 302.00 303.00 308.00 313.00 318.00 323.00 328.00 333.00 338.00 343.00 353.00 363.00 365.00 367.00 369.00 371.00 Inverse Absolute temp (1/K) 0.003663004 0.003597122 0.003533569 0.003508772 0.003484321 0.003460208 0.003448276 0.003436426 0.003424658 0.003412969 0.003401361 0.003389831 0.003378378 0.003367003 0.003355705 0.003344482 0.003333333 0.003322259 0.003311258 0.00330033 0.003246753 0.003194888 0.003144654 0.003095975 0.00304878 0.003003003 0.00295858 0.002915452 0.002832861 0.002754821 0.002739726 0.002724796 0.002710027 0.002695418 VP (mmHg) 4.58 6.54 9.21 10.52 11.99 13.63 14.53 15.48 16.48 17.54 18.65 19.83 21.07 22.38 23.76 25.21 26.74 28.35 30.04 31.82 42.20 55.30 71.90 92.50 118.00 149.40 187.50 233.70 255.10 525.80 567.00 610.90 657.60 707.30 Natural log of VP 1.521698998 1.877937165 2.22028985 2.353278207 2.484072969 2.612273246 2.676215478 2.739548868 2.802147524 2.864483987 2.925846146 2.987195943 3.047850228 3.108167703 3.168003494 3.227240741 3.286160572 3.34462703 3.402529827 3.460095023 3.742420221 4.012772909 4.275276265 4.527208645 4.770684624 5.006627273 5.233778845 5.454038242 5.541655625 6.264920912 6.340359304 6.41493328 6.488596844 6.561454904 50.00 55.00 60.00 65.00 70.00 80.00 90.00 92.00 94.00 96.00 98.00