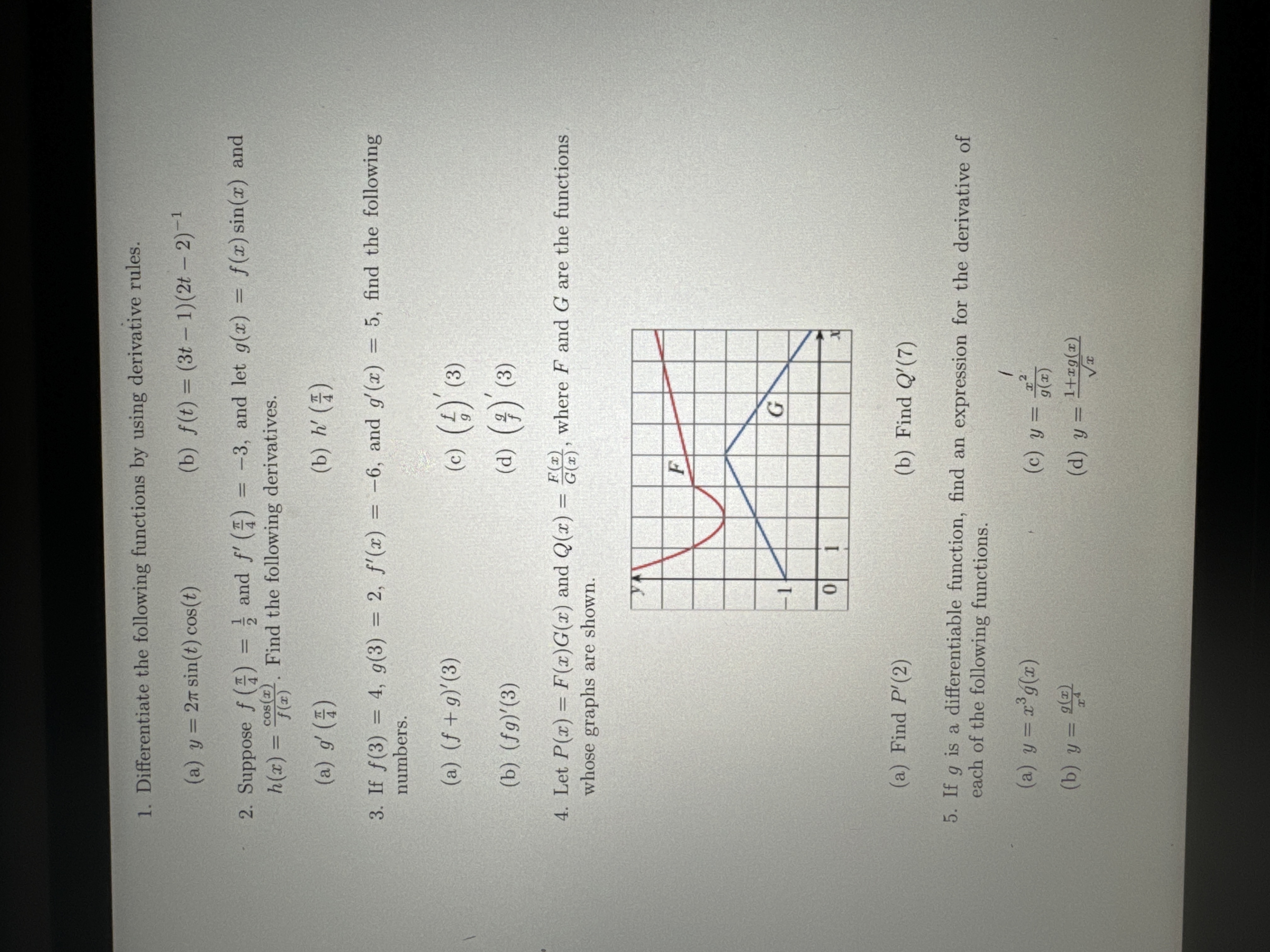
1. Differentiate the following functions by using derivative rules. (a) y = 27 sin(t) cos(t) ( b ) f ( t ) = ( 3t - 1 ) ( 2t - 2 ) - 1 2. Suppose f (#) = ; and f' (7) = -3, and let g(x) = f(x) sin(x) and h(x) = cos(z) (x) . Find the following derivatives. (a) g' (#) (b) h ( # ) 3. If f(3) = 4, g(3) = 2, f'(x) = -6, and g'(x) = 5, find the following numbers. (a) (f + g)'(3) (c ) (; ) (3) (b) (fg)' (3) (d) (;) (3) 4. Let P(x) = F(x)G(x) and Q(x) = G(x) , W F(x) where F and G are the functions whose graphs are shown. F G 0 (a) Find P' (2) (b) Find Q'(7) 5. If g is a differentiable function, find an expression for the derivative of each of the following functions. (a) y = x'g(x) ( c ) y = 3 2 2 g(x) ( b) y = (x) (d) y = ltrg(x) Vx