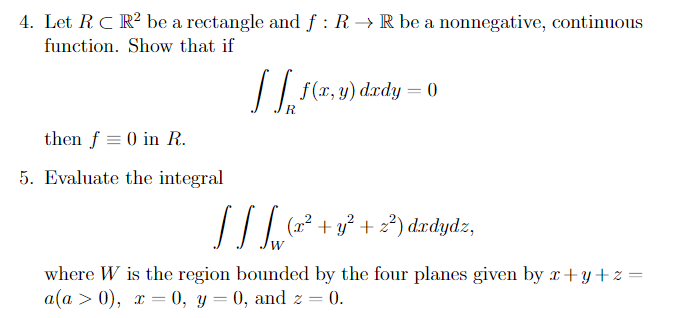
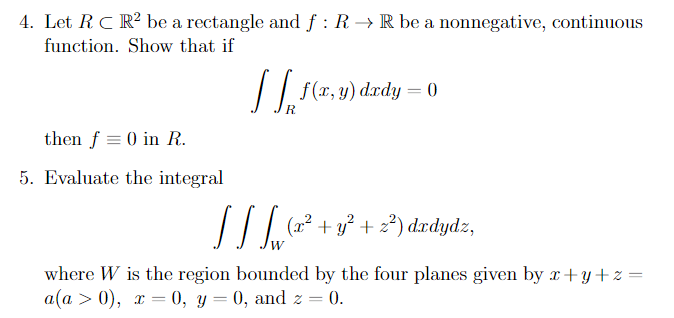
1. Evaluate the double integral cos y drdy where the region D is bounded by y = 2x, y = x, x = 1, and x = 2x. 2. Change the order of integration and evaluate sin(x ) daxdy. 3. Find the integral through change the order of integration dady. Jy/24. Let R C R' be a rectangle and f : R -> R be a nonnegative, continuous function. Show that if f(x, y) dady = 0 then f = 0 in R. 5. Evaluate the integral (12 + 32 + 2?) drdydz, W where W is the region bounded by the four planes given by a ty + z = a(a > 0), x =0, y = 0, and z = 0