Question: 1 Find equations tor the tangent plane and the normal line at peint PD (Neil'qzuj (4.5: E1) on the surface - Sees [EX] +2331; +
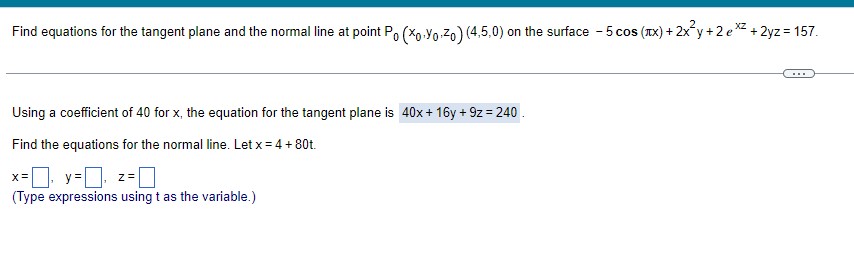
![at peint PD (Neil'qzuj (4.5: E1) on the surface - Sees [EX]](https://s3.amazonaws.com/si.experts.images/answers/2024/06/6665fedd7c9b9_4136665fedd5807b.jpg)


1
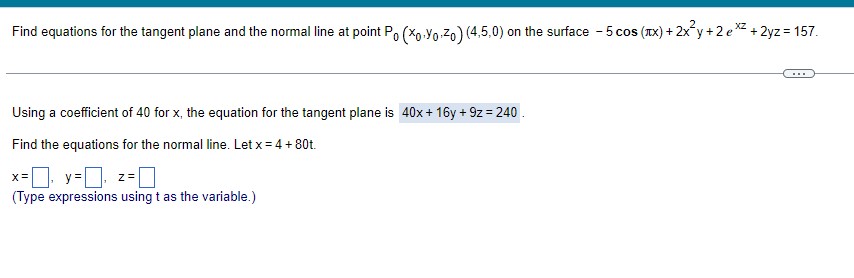
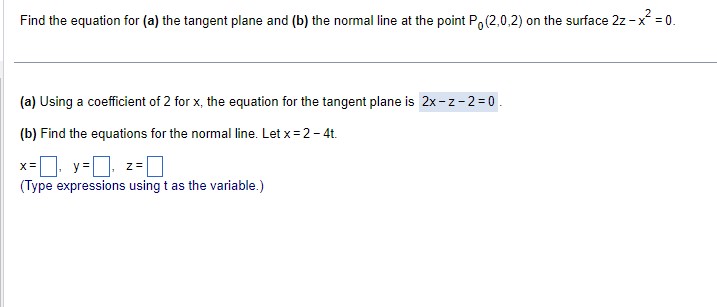
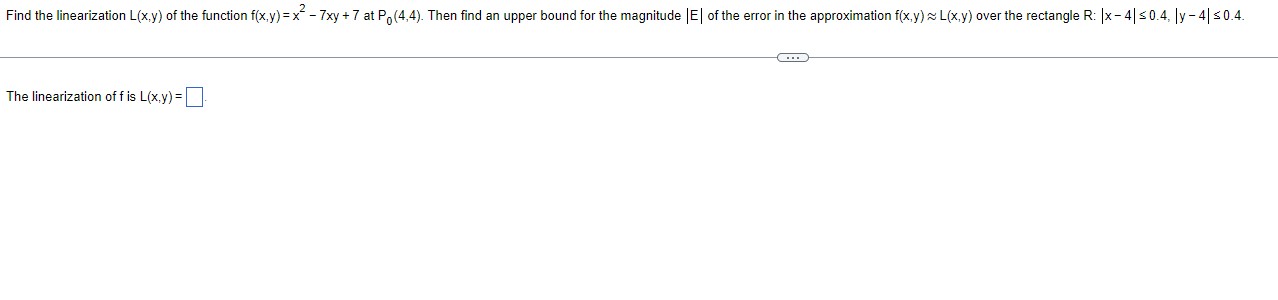


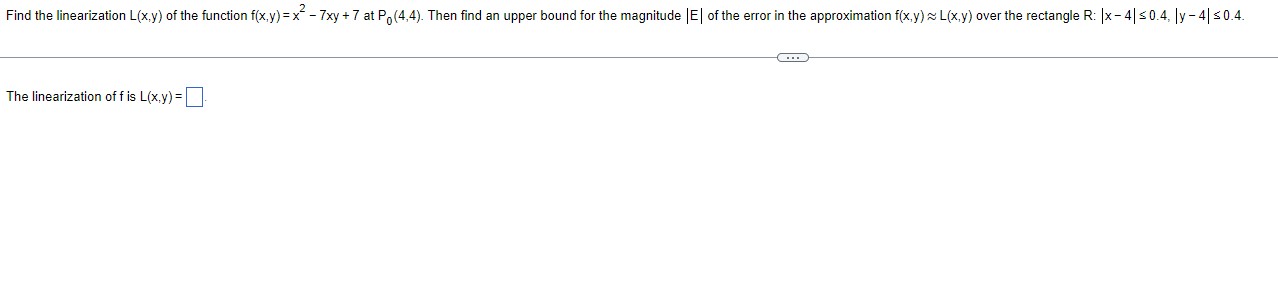
Find equations tor the tangent plane and the normal line at peint PD (Neil'qzuj (4.5: E1) on the surface - Sees [EX] +2331; + 2 an + 23;: =15? :} Using a coefficient of 40 for x, the equation for the tangent plane is 40x+16y + 92: 24D. Find the equations fer the normal line. Let x =4 + BUt. K: II yzl I 2: Type expressions using t as the variable.) Find the equation for (a) the tangent plane and (b) the normal line at the point P. (2,0,2) on the surface 2z - x" = 0. (a) Using a coefficient of 2 for x, the equation for the tangent plane is 2x - z - 2 = 0 (b) Find the equations for the normal line. Let x = 2 - 4t. X= y = Z = (Type expressions using t as the variable.)Find the linearization L(x,y) of the function f(x,y) = x- - 7xy + 7 at P. (4,4). Then find an upper bound for the magnitude | E| of the error in the approximation f(x,y) ~ L(x,y) over the rectangle R: |x - 4| $ 0.4, ly - 4| $ 0.4. The linearization of f is L(x.y) =].Suppose that T is to be found from the formula T=y(e*+ e "*), where x and y are found to be In 2 and 2 with maximum possible errors of | dx) = 0.05 and | dy) = 0.1. Estimate the maximum possible error in the computed value of T. The magnitude of the estimated maximum possible error is. (Type an integer or a decimal.)Complete the ordered triple. Write the solution as an ordered triple. Select the correct choice below and fill in any answer boxes within your choice. 9x - y+ z = -6 2x + 2y - 3z = 17 O A. There is one solution, ( D). x - 3y + 2z = - 13 (Type exact answers in simplified form.) O B. The system is dependent. O C. There is no solution
Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


