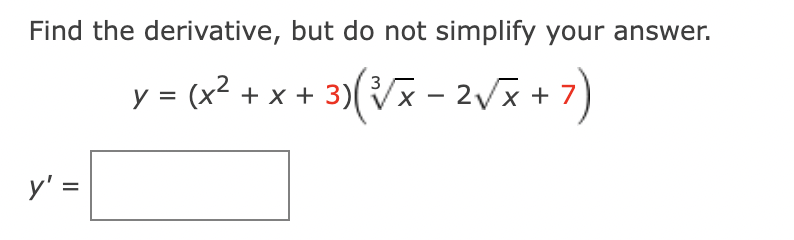
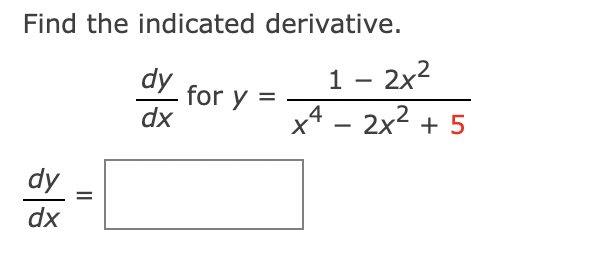
1. Find the derivative and simplify.

y = (8x + 5)(x² 3x).

2. Find the derivative and simplify.

y = (4x⁷ + 5)(9x⁶ 7x⁴ 5)

dy/dx=

3. Find the derivative, but do not simplify your answer.

y = (5x⁶ 3x⁴ + 2x² 1)(4x⁸ + 3x⁶ 5x² + 4x)

y=

4. see picture

5. For the function

y = (x² + 3)(x³ 4x), at (2, 0) find the following.

(a) the slope of the tangent line (b) the instantaneous rate of change of the function

6. see picture

7. see picture

8. see picture

9. Write the equation of the tangent line to the graph of y = (8x² 6x + 1)(1 + 2x) at x = 1. Check the reasonableness of your answer by graphing both the function and the tangent line.

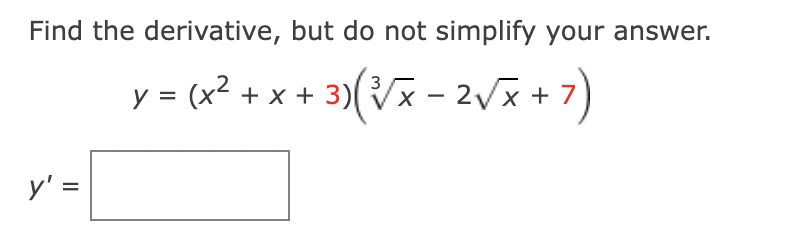
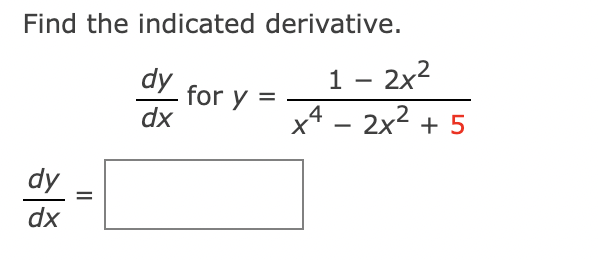
\fConsider the following. Let u(q) = q2 + 4 and v(q) = 4a 1. Find each indicated derivative. U'(q) = v'(q) = UH Find each indicated product. V0?) ' 0'0?) = U(q) - W?) = UH