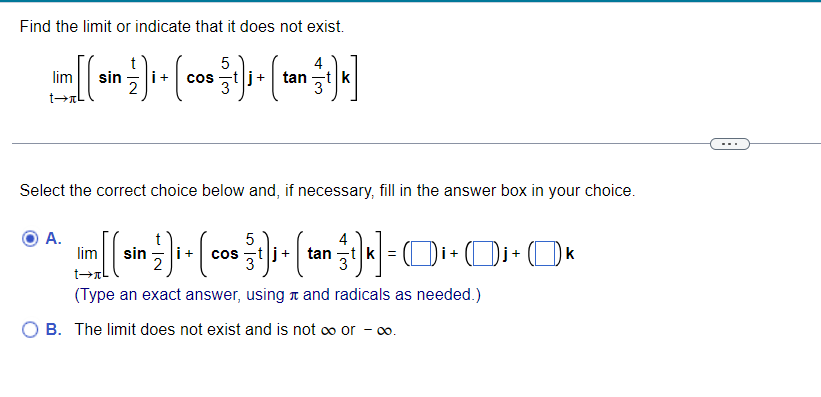
Question: 1. Find the limit or indicate that it does not exist. dime[costlrltaslkl Select the correct choice below and, if necessary; ll in the answer box

![exact answer, using If. and radicals as needed.) If] E. The limit](https://s3.amazonaws.com/si.experts.images/answers/2024/06/667b51931eb5d_843667b51930a208.jpg)
1.


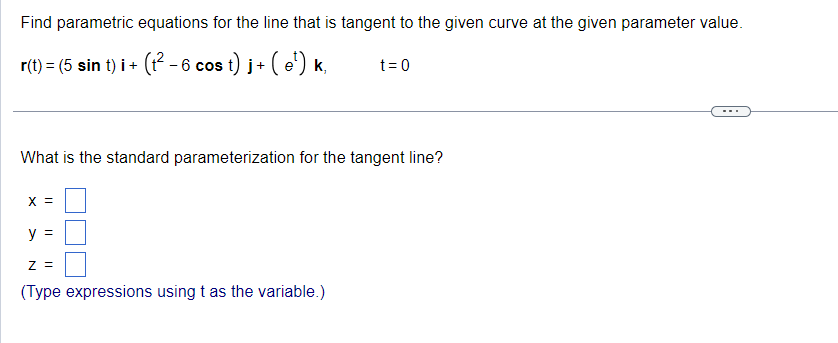
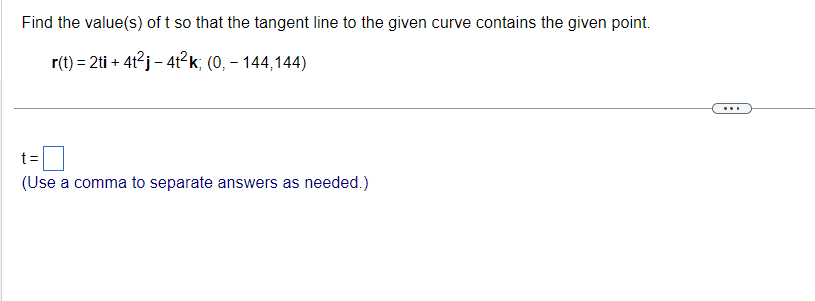
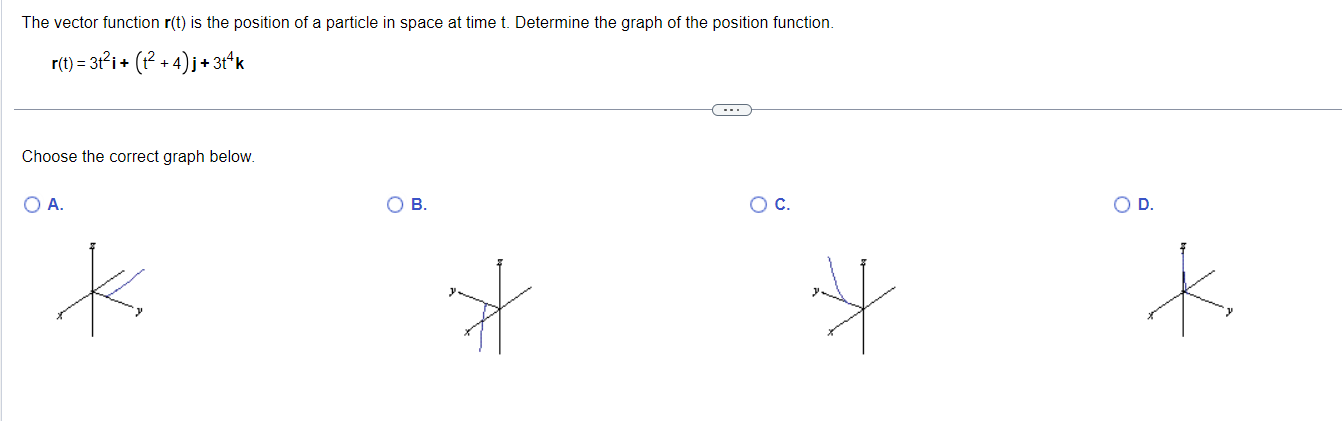
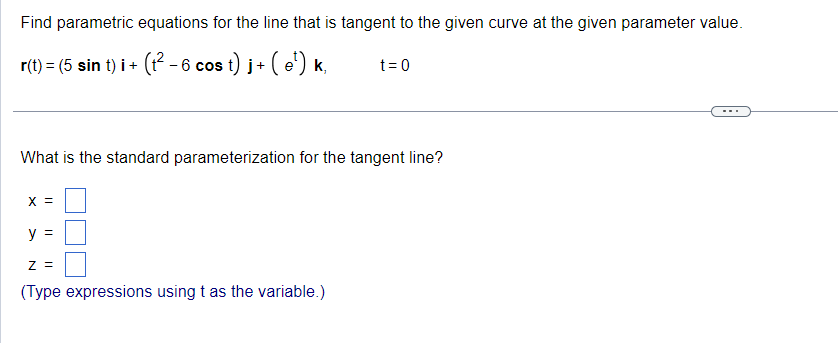
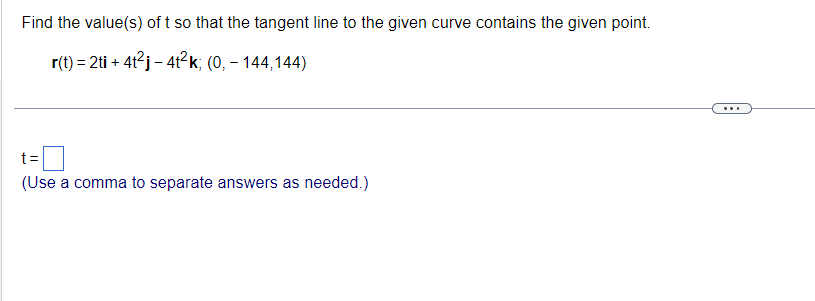
Find the limit or indicate that it does not exist. dime\"[costlrltaslkl Select the correct choice below and, if necessary; ll in the answer box in your choice. \"miitgticosgtl[marl M M l tH'E (Type an exact answer, using If. and radicals as needed.) If] E. The limit does not exist and is not on or oo. The position of a particle in space at time t is r(t) as shown below. Find the particle's velocity and acceleration vectors. Then find the particle's speed and direction of motion at t= 1. Write the particle's velocity at that time as the product of its speed and direction. r(t) = (3 In (t + 1))i + +2j +- The velocity vector is v(t) =i + + k. (Type exact answers, using radicals as needed.)2 2 The equation rtt) = [7t] i + [gt1&2] j is the position of a particle in space at time t. Find the angle between the velocity and acceleration vectors at time t2 O. The angle between the velocity and acceleration vectors at time t : 0 is radians (Type an exact answer, using I: as needed J Find parametric equations for the line that is tangent to the given curve at the given parameter value. r(t) = (5 sin t) i + (tz -6 cost) j+ ( et) k, t= 0 What is the standard parameterization for the tangent line? X = V = Z = (Type expressions using t as the variable.)Find the value(s) of t so that the tangent line to the given curve contains the given point. r(t) = 2ti + 4t2j - 412k; (0, - 144,144) t = (Use a comma to separate answers as needed.)The vector function r(t) is the position of a particle in space at time t. Determine the graph of the position function. r(t) = 312i + (+2 + 4) j + 3+4k . . . Choose the correct graph below. O A. O B. O c. OD. y. K
Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


