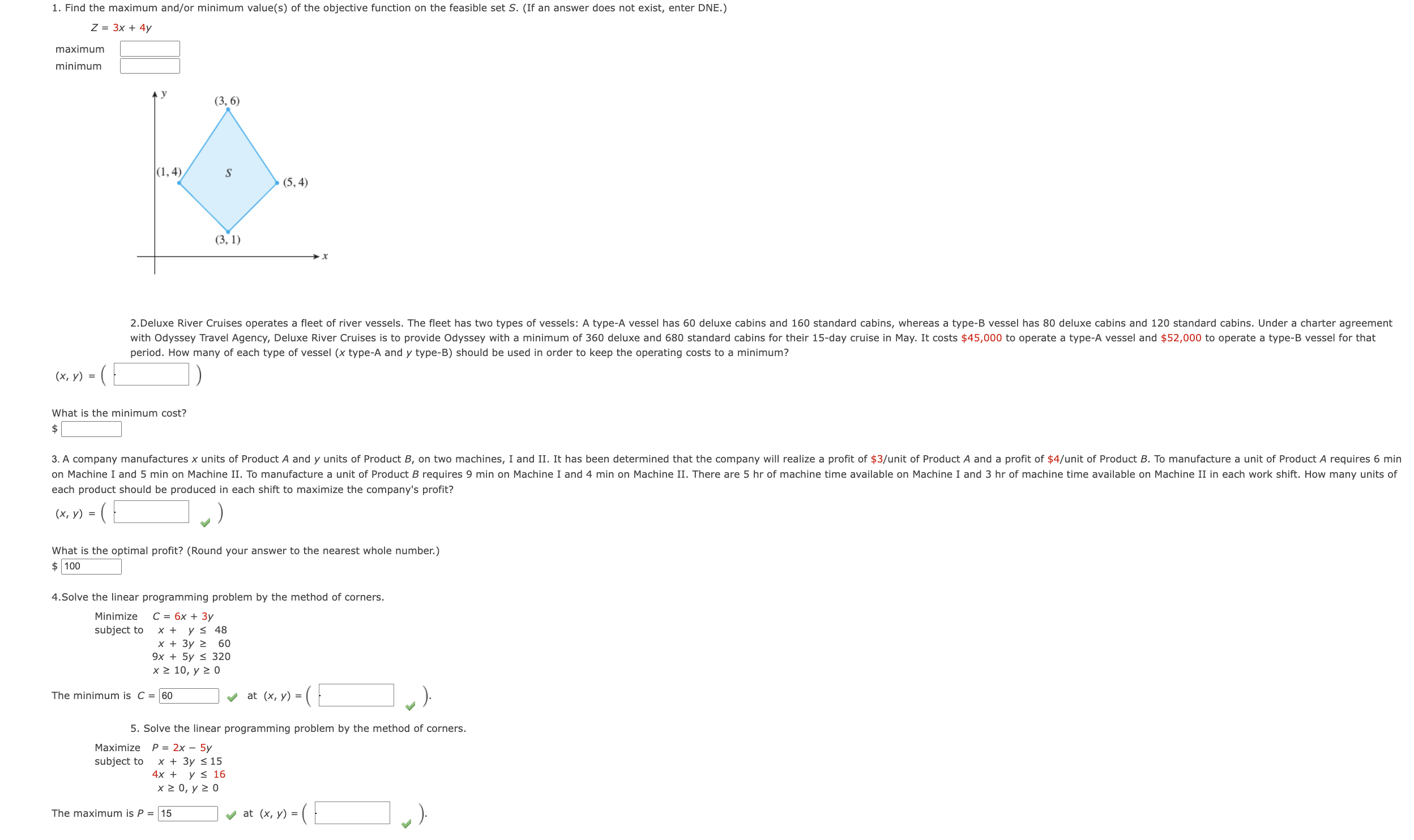
1. Find the maximum and/or minimum value(s) of the objective function on the feasible set S. (If an answer does not exist, enter DNE.) Z = 3x + 4y maximum minimum (3, 6) (1, 4 S (5, 4) (3, 1) 2. Deluxe River Cruises operates a fleet of river vessels. The fleet has two types of vessels: A type-A vessel has 60 deluxe cabins and 160 standard cabins, whereas a type-B vessel has 80 deluxe cabins and 120 standard cabins. Under a charter agreement with Odyssey Travel Agency, Deluxe River Cruises is to provide Odyssey with a minimum of 360 deluxe and 680 standard cabins for their 15-day cruise in May. It costs $45,000 to operate a type-A vessel and $52,000 to operate a type-B vessel for that period. How many of each type of vessel (x type-A and y type-B) should be used in order to keep the operating costs to a minimum? ( x, y) = ( What is the minimum cost? $ 3. A company manufactures x units of Product A and y units of Product B, on two machines, I and II. It has been determined that the company will realize a profit of $3/unit of Product A and a profit of $4/unit of Product B. To manufacture a unit of Product A requires 6 min on Machine I and 5 min on Machine II. To manufacture a unit of Product B requires 9 min on Machine I and 4 min on Machine II. There are 5 hr of machine time available on Machine I and 3 hr of machine time available on Machine II in each work shift. How many units of each product should be produced in each shift to maximize the company's profit? ( x, y ) = (L What is the optimal profit? (Round your answer to the nearest whole number.) $ 100 4.Solve the linear programming problem by the method of corners. Minimize C = 6x + 3y subject to x + y s 48 x + 3y 2 60 9x + 5y S 320 x 2 10, y 2 0 The minimum is C = 60 at (x, y) = ( 5. Solve the linear programming problem by the method of corners. Maximize P = 2x - 5y subject to x + 3y s 15 4x + y s 16 x20, y 20 The maximum is P = 15 at (x, y) = (