1) Given an n-element array X, Algorithm D calls Algorithm E on each element X[i]. Algorithm E runs in O(i) time when it is called on element X[i]. What is the worst case running time of Algorithm D?

Please explain why each algorithm is a certain time complexity.

2)

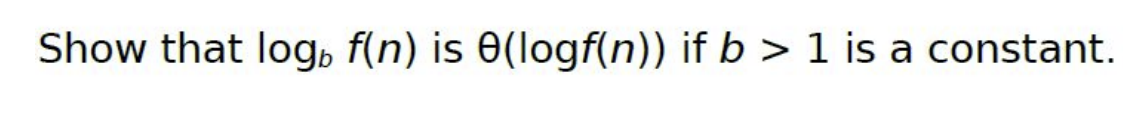
3) Describe a method for finding both the minimum and maximum of an array of n numbers using fewer than 3n/2 comparisons. (Hint: first construct a group of candidate minimums and a group of candidate maximums)

4)

Show that logbf(n) is (logf(n)) if b>1 is a constant. Bob built a Web site and gave the URL only to his n friends, which he numbered from 1 to n. He told friend number i that he/she can visit the Web site at most i times. Now Bob has a counter, C, keeping track of the total number of visits to the site (but not the identities of who visits). What is the minimum value for C such that Bob should know that one of his friends has visited his/her maximum allowed number of times