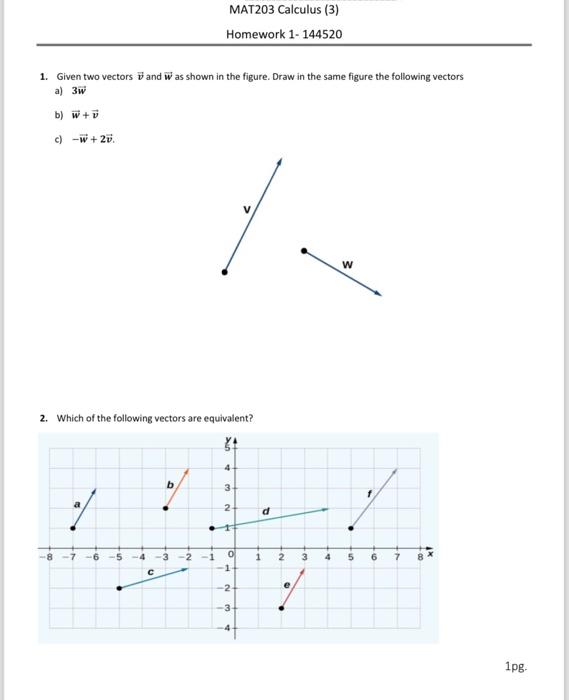
1. Given two vectors v and W as shown in the figure. Draw in the same figure the following vectors a) 3w b) w+v c) w+2v. 2. Which of the following vectors are equivalent? 3. Suppose that ||v^=3 and =3. (a) Write v~ in component form and form of standard unit vectors (b) Find a unit vector with same direction as v. (c) Find a vector w with opposite direction as as v such that magnitude of W is 5 . 4. Consider two points A(3,1,5) and B(2,1,1). (a) Sketch the both points. (b) Find distance between A and B. (c) Write an equation of the line through A and B. (d) Write the vector AB in component form and in the form of standard unit vector. (e) Find the standard equation of the sphere with diammeter AB. (f) Write an equation of the plane passing through A and parallel to yz-plane. (g) Write an equation of the plane containing the points A,B and the origin. 5. Find the center and radius of the sphere with an equation in general form that is given by 4x2+y28y+z2+4z+1=0 6. Find the terminal point A of the vector BA=7,1,3) where B(2,3,5). 7. Find all value(s) of t for which p=(2,3,4) is orthogonal to q=(x4,3,1). 8. Consider the line defined by the symmetric equations: 4x3=2y+1=z3. (a) Find parametric equations of the line. (b) Compute the distance between the point (1,1,3) and the line. 9. Show that pq is orthogonal to (pq)(p+q)+q. 10. Consider the box as shown in the figure. (a) Find the coordinate of all vertices. (b) Compute the volume of the box without using the cross product. (c) Use the cross product to find the volume of the box. 11. Find an equation of the plane containing the lines L1: x=y=x L2: 2x3=y=x2 12. (Research question): Let u=(u1,u2,u3),v=v1,v2,v3) and w=w1,w2,w3 be three vectors. (a) Prove that the triple scalar product u. (iv w) is equal to u1v1w1w2w2w2w3w3w1 (b) Use the triple scalar product to find the volume of the parallelepiped defined by the adjacent edges u=0,5,2),v=(1,2,1) and w=(4,3,2). (c) Prove that three vectors are coplanar (all lle in the same plane), if their triple scalar product is zero. 13. Compute the distance between the point (3,1,2) and the plan given by: x2y+z=5. 14. Find the angle between the planes defined by: x+y+z=1 and 2xy+z=1 15. 15. Determine whether each pair of planes is parallel, orthogonal, or neither. (a) x+2yz=8 and 2x+4y2z=1. (b) 6x+2y3z=1 and 2z3y+2x3=0. (c) x3y+5z=1 and x+y+x=4