Question: 1. Given. v = 21 +3j + k and w = 51 +4j -3k, find a vector perpendicular to the planef2. Let f(x,y) = By'
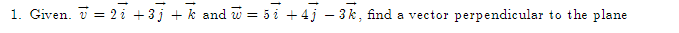
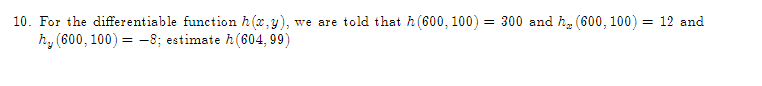
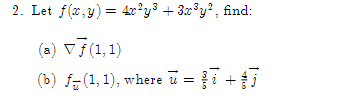
![where u3. The population density of a circular city of diameter ll]](https://s3.amazonaws.com/si.experts.images/answers/2024/06/666467791de85_121666467790cb6c.jpg)
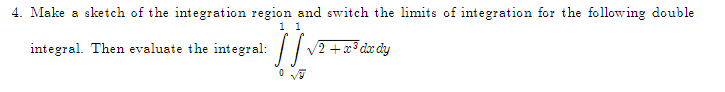

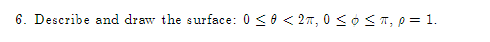
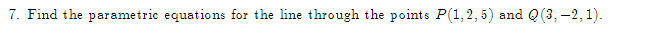

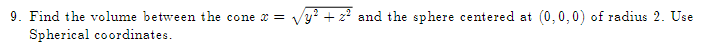
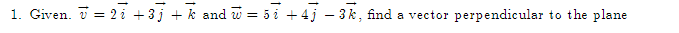
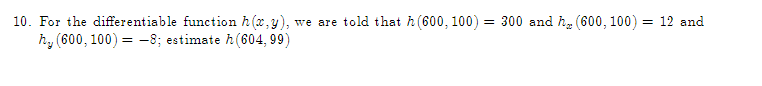
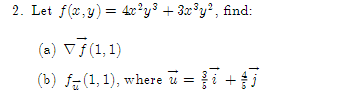

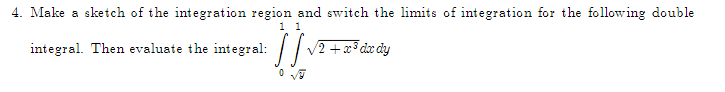
![sphere centered at III: UFCI] of radius 2. Use Spherical eeerdinetes](https://s3.amazonaws.com/si.experts.images/answers/2024/06/6664677c68a63_1246664677c57465.jpg)
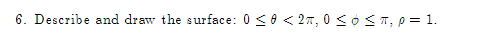
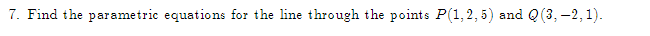

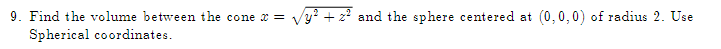
1. Given. v = 21 +3j + k and w = 51 +4j -3k, find a vector perpendicular to the plane\f2. Let f(x,y) = By' + 3xly', find: Vf (1, 1) (b) f- (1, 1), where u3. The population density of a circular city of diameter ll] miles varies linearly front l people per square mile at the center of the city to [I people per square mile on the outer boundary. Set up an integral that represents the total population of the city. Evaluate the integral. 4. Make a sketch of the integration region and switch the limits of integration for the following double 1 1 integral. Then evaluate the integral: V2 + x'drdy 0 vy5. Evaluate ffxg y2 dxdy: 1:L'he:l*e R is the top half of a ring between two circles: one of radius 2 F and the other of radius 3: both centered at the origin. \f7. Find the parametric equations for the line through the points P(1, 2, 5) and Q(3, -2, 1).\f9. Find the volume between the cone .1: 2 y? z? and the sphere centered at III: UFCI] of radius 2. Use Spherical eeerdinetes
Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


