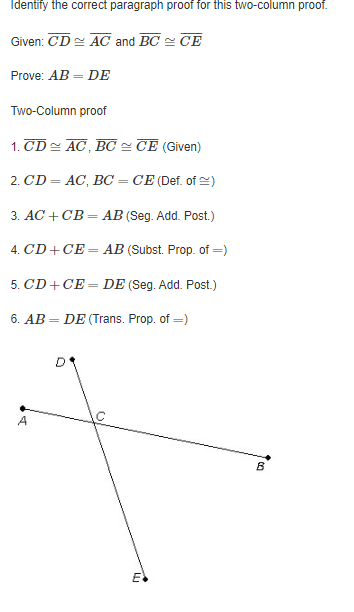
Question: 1. Identify the correct paragraph proof for this two-column proof. Given: CD ~ AC and BC ~ CE Prove: AB = DE Two-Column proof 1.
1.
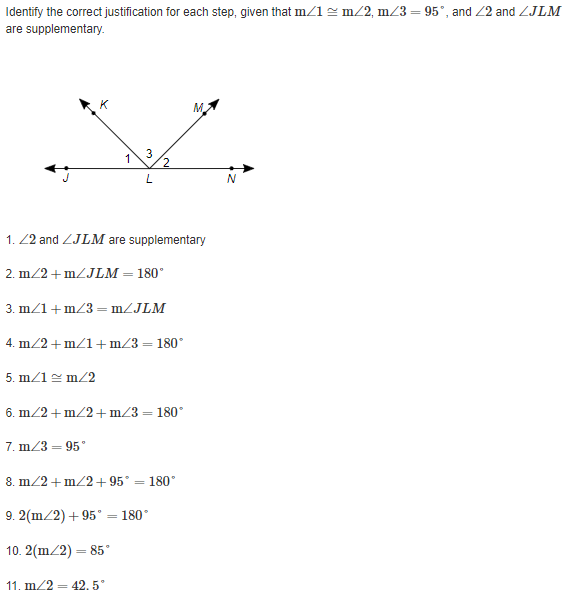
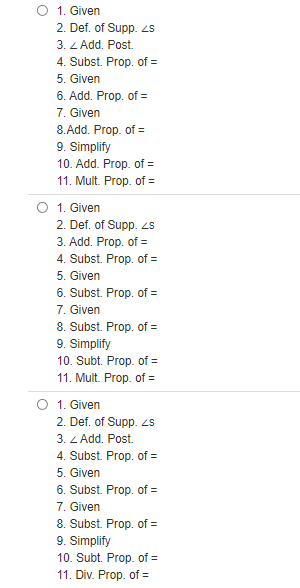
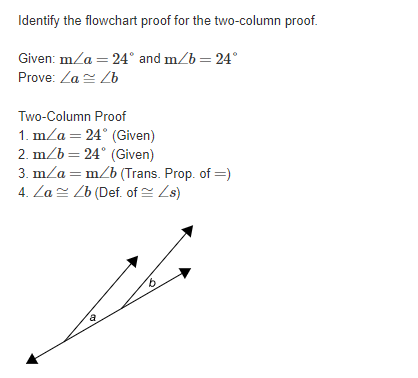
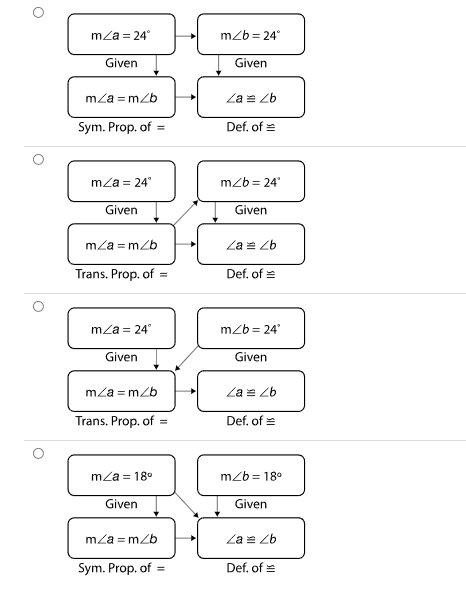
Identify the correct paragraph proof for this two-column proof. Given: CD ~ AC and BC ~ CE Prove: AB = DE Two-Column proof 1. CD ~ AC, BC ~ CE (Given) 2. CD = AC, BC = CE (Def. of ~ ) 3. AC + CB = AB (Seg. Add. Post.) 4. CD + CE = AB (Subst. Prop. of =) 5. CD + CE = DE (Seg. Add. Post.) 6. AB = DE (Trans. Prop. of =) A C BO It is given that line segments CD and AC are congruent, as well as line segments BC and CE. So, by the definition of congruence, the lengths of line segments CD and AC are equal, as well as BC and CE. By the Segment Addition Postulate, AC + CB = AB. It follows that by the Substitution Property of Equality, CD + CE = AB since AC = CD and BC = CE. Again, by the Segment Addition Postulate, CD + CE = DE. Therefore, by the Transitive Property of Equality, AB = DE. O It is given that line segments CD and AC are congruent, as well as line segments BC and CE. So, by the definition of congruence, the lengths of line segments CD and BC are equal, as well as AC and CE. By the Segment Addition Postulate, AC + CB = AB. It follows that by the Substitution Property of Equality, CD + CE = AB since AC = CD and BC = CE. Again, by the Segment Addition Postulate, CD + CE = DE. Therefore, by the Transitive Property of Equality, AB = DE. O It is given that line segments CD and AC are congruent, as well as line segments BC and CE. So, by the definition of congruence, the lengths of line segments CD and BC are equal, as well as AC and CE. By the Segment Addition Postulate, AC + CD = AB. It follows that by the Substitution Property of Equality, CE + BC = AB since AC = CE and BC = CD. Again, by the Segment Addition Postulate, CE + BC = DE. Therefore, by the Transitive Property of Equality, AB = DE.Identify the correct justification for each step, given that m/1 ~ m/2, m/3 =95, and Z2 and ZJLM are supplementary. K 2 L N 1. /2 and ZJLM are supplementary 2. m/2 + m/JLM = 180 3. m/1 + m/3= m/JLM 4. m/2 +m/1+ m/3 =180 5. m/1 ~ m/2 6. m/2 +m/2+ m/3 =180 7. m/3 = 95 8. m/2 + m/2+95* = 180 9. 2(m/2) + 95* = 180* 10. 2(m/2) = 85 11. m/2 = 42.5O 1. Given 2. Def. of Supp. 25 3. 2 Add. Post. 4. Subst. Prop. of = 5. Given 6. Add. Prop. of = 7. Given 8.Add. Prop. of = 9. Simplify 10. Add. Prop. of = 11. Mult. Prop. of = O 1. Given 2. Def. of Supp. 25 3. Add. Prop. of = 4. Subst. Prop. of = 5. Given 6. Subst. Prop. of = 7. Given 8. Subst. Prop. of = 9. Simplify 10. Subt. Prop. of = 11. Mult. Prop. of = O 1. Given 2. Def. of Supp. 25 3. 2 Add. Post. 4. Subst. Prop. of = 5. Given 6. Subst. Prop. of = 7. Given 8. Subst. Prop. of = 9. Simplify 10. Subt. Prop. of = 11. Div. Prop. of =O 1. Given 2. Lin. Pair Thm. 3. 2 Add. Post. 4. Subst. Prop. of = 5. Vert. 2s Thm. 6. Subst. Prop. of = 7. Given 8. Subst. Prop. of = 9. Simplify 10. Subt. Prop. of = 11. Div. Prop. of =O 179-7 =7(g- 11) Given 17g -7 =79-77 Sym. Prop. of = 10g -7 =-77 Sub. Prop. of = 10g = -70 Reflex. Prop. of = 9= -7 Div. Prop. of = O 179-7 =7(g -11) Given 179-7=79-77 Distribprop. of = 10g - 7 =-77 Sub. Prop. of = 10g = 70 Substitution Prop. of = 9=7 Div. Prop. of = O 179- 7 =7(g- 11) Given 179 -7 =7g -77 Distribrop. of = 10g -7 = -77 Sub. Prop. of = 10g =-70 Add. Prop. of = 9= -7 Div. Prop. of = O 17g-7 =7(g-11) Given 179-7 =7g - 77 Distribprop. of = 10g -7 = -77 Add. Prop. of = -10g = -70 Add. Prop. of = 9=7 Div. Prop. of =Identify the flowchart proof for the two-column proof. Given: ma = 24" and m/b = 24" Prove: Za~ Zb Two-Column Proof 1. ma = 24 (Given) 2. m/b = 24" (Given) 3. ma = m/b (Trans. Prop. of =) 4. Za ~ Zb (Def. of = /s) b HO mza = 24* myb =24" Given Given mZa =m/b La = Zb Sym. Prop. of = Def. of = O mza = 24" myb =24" Given Given mza = m/b La = Zb Trans. Prop. of = Def. of = O mza = 24" myb = 24" Given Given mZa = m/b Za = Zb Trans. Prop. of = Def. of = O mza = 180 myb =180 Given Given mZa =m/b La = /b Sym. Prop. of = Def. of =